- 二元二次方程表示圆的条件
- 共80题
若抛物线


正确答案
解析

知识点
如图5,









。
正确答案
解析
略
知识点
已知函数f(x)=ex-ln(x+m)。
(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;
(2)当m≤2时,证明f(x)>0.
正确答案
见解析
解析
(1)f′(x)=
由x=0是f(x)的极值点得f′(0)=0,所以m=1.
于是f(x)=ex-ln(x+1),定义域为(-1,+∞),f′(x)=
函数f′(x)=
因此当x∈(-1,0)时,f′(x)<0;
当x∈(0,+∞)时,f′(x)>0.
所以f(x)在(-1,0)单调递减,在(0,+∞)单调递增。
(2)当m≤2,x∈(-m,+∞)时,ln(x+m)≤ln(x+2),故只需证明当m=2时,f(x)>0.
当m=2时,函数f′(x)=
又f′(-1)<0,f′(0)>0,
故f′(x)=0在(-2,+∞)有唯一实根x0,且x0∈(-1,0)。
当x∈(-2,x0)时,f′(x)<0;
当x∈(x0,+∞)时,f′(x)>0,从而当x=x0时,f(x)取得最小值。
由f′(x0)=0得

故f(x)≥f(x0)=

综上,当m≤2时,f(x)>0
知识点
若从1,2,2,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有
正确答案
解析
1,2,2,…,9这9个整数中有5个奇数,4个偶数,要想同时取4个不同的数其和为偶数,则取法有:
4个都是偶数:1种;
2个偶数,2个奇数:
4个都是奇数:
∴不同的取法共有66种。
知识点
函数
正确答案
解析
略
知识点
设












正确答案
解析
略。
知识点
与圆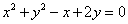
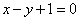
正确答案
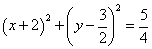
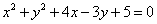
解析
圆C的标准方程为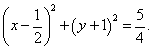
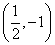
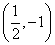

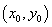
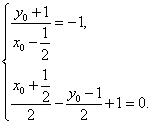
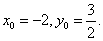

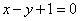
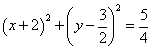
知识点
设函数
(1)画

(2)若不等式

正确答案
见解析。
解析
(1)由于
则函数
(2)由函数

当且仅当

函数

故不等式



知识点
等差数列{an}的前n项和为Sn,已知S10=0,S15=25,则nSn的最小值为__________。
正确答案
-49
解析
设数列{an}的首项为a1,公差为d,则S10=
S15=
联立①②,得a1=-3,
所以Sn=
令f(n)=nSn,则

令f′(n)=0,得n=0或
当


知识点
方程
正确答案
解析
略
知识点
扫码查看完整答案与解析














