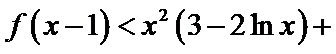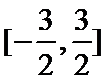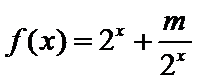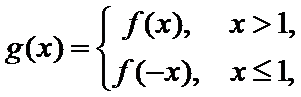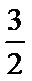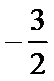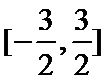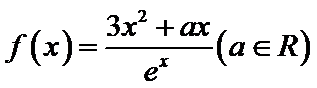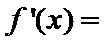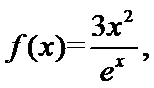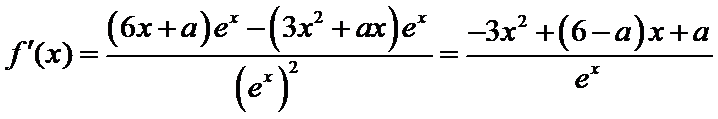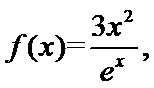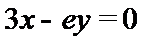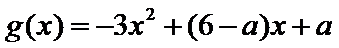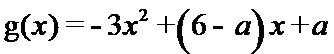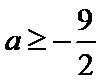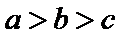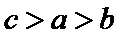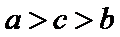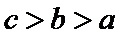- 函数奇偶性的性质
- 共128题
已知函数f(x)是定义在R上的周期为2的奇函数,当0<x<1时,f(x)=

正确答案
-2
知识点
8.设函数

正确答案
解析
显然,f(x)的定义域为(-1,1),关于原点对称,又
考查方向
解题思路
分求函数的定义域后发现其关于原点对称,后利用奇偶性的定义得到其为奇函数,最后利用奇函数在对称的区间上单调性相同,得到其单调性。
易错点
对于函数的性质不理解导致出错。
知识点
10.已知R上的奇函数


正确答案
解析
设
则
设 




∵

即

则不等式


则x<1,即不等式
∴所以选项B为正确选项
考查方向
解题思路
构造函数g(x),求函数的导数,判断函数的单调性,利用函数的单调性进行求解即可.
易错点
构造函数g(x)错误
知识点
12.设函数f’(x)是奇函数f (x)(x∈R)的导函数,f(-1)=0,当x>0时,x f’(x)-f (x)<0,则使得f (x) >0成立的x的取值范围是( )
正确答案
知识点
设函数





26.求


27.设


正确答案

解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,由函数的奇偶性形成方程组求解出



联立①②解得





考查方向
解题思路
本题考查导数的应用,解题步骤如下:函数的奇偶性形成方程组求解出
易错点
对求解析式方法不熟导致出错。
正确答案
详见解析;
解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,由函数的奇偶性形成方程组求解出



联立①②解得





考查方向
解题思路
本题考查导数的应用,解题步骤如下:
观察所证不等式的结构构建新函数去证明所求不等式。
易错点
未发现
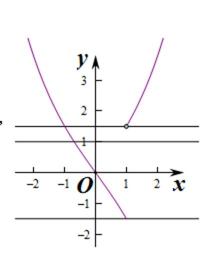
13.设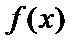
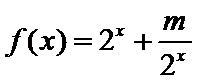
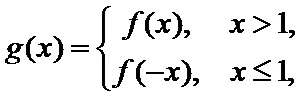
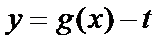
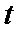
正确答案
解析
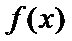
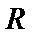
则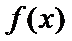
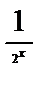
则当x>1时,函数为增函数,且当x
当x 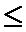


由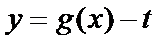
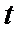
考查方向
解题思路
函数与方程的思想,将函数的零点转化为方程的解、两个函数的交点,用函数的图形来处理。
易错点
1、对零点概念、方程与函数的思想理解不到位,不能准确地转化为函数来处理。
2、本题不容易理解有且只有一个零点含义,从而造成求解上的不精确。。
知识点
(本小题满分12分,(1)小问7分,(2)小问5分)
设函数
23.若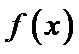
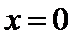
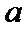
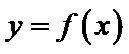
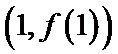
24.若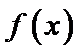
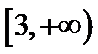
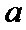
正确答案
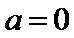
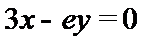
解析
试题分析:本题考查求复合函数的导数,导数与函数的关系,由求导法则可得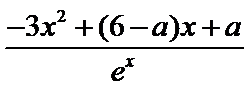
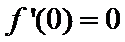
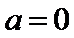
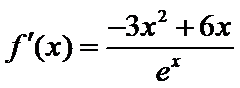
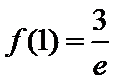
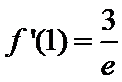
试题解析:(1)对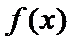
因为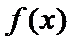
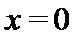
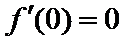
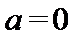
当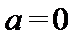
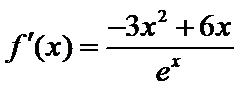
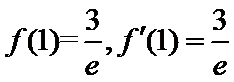
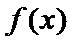
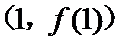
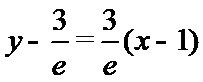
考查方向
解题思路
导数及其应用通常围绕四个点进行命题.第一个点是围绕导数的几何意义展开,设计求曲线的切线方程,根据切线方程求参数值等问题,这类试题在考查导数的几何意义的同时也考查导数的运算、函数等知识,试题的难度不大;第二个点是围绕利用导数研究函数的单调性、极值(最值)展开,设计求函数的单调区间、极值、最值,已知单调区间求参数或者参数范围等问题,在考查导数研究函数性质的同时考查分类与整合思想、化归与转化思想等数学思想方法.
易错点
极值的几何意义.
正确答案
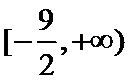
解析
试题分析:(2)由题意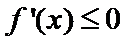
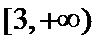
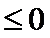
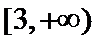
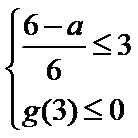
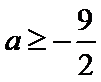
试题解析:(2)由(1)得,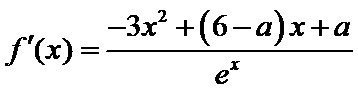
令
由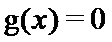
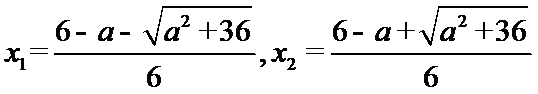
当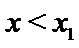
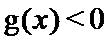
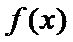
当
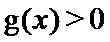
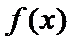
当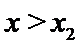
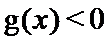
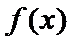
由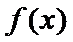
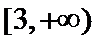
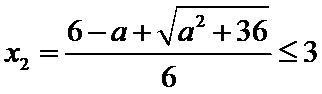
故a的取值范围为
考查方向
解题思路
导数及其应用通常围绕四个点进行命题.第三个点是围绕导数研究不等式、方程展开,涉及不等式的证明、不等式的恒成立、讨论方程根等问题,主要考查通过转化使用导数研究函数性质并把函数性质用来分析不等式和方程等问题的能力,该点和第二个点一般是解答题中的两个设问,考查的核心是导数研究函数性质的方法和函数性质的应用;第四个点是围数性质并把函数性质用来分析不等式和方程等问题的能力,该点和第二个点一般是解答题中的两个设问,考查的核心是导数研究函数性质的方法和函数性质的应用;
易错点
本题涉及第一个点和第二个点,主要注意问题的转化,转化为不等式恒成立,转化为二次函数的性质.
10.奇函数




正确答案
解析
考查方向
解题思路
该题解题思路
1)

2)根据对称性得出函数为周期函数,周期T=4
3)利用周期性易得取值
易错点
主要易错于

知识点
13.已知函数f(x)=(9x+1)·9kx(k∈R)为偶函数,则实数k的值为 .
正确答案
解析
由题意知






考查方向
解题思路
由于函数为偶函数,所以有



易错点
对偶函数的定义理解不清导致出错。
知识点
10.已知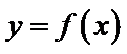
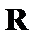
且当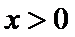
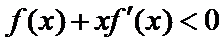
若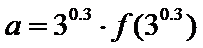
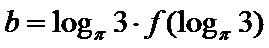
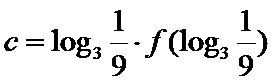
则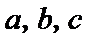
正确答案
解析
试题分析:令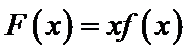
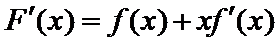
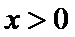
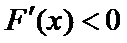
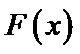
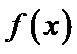
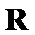
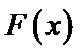
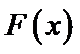
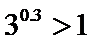
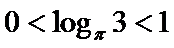
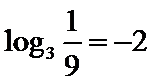
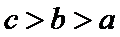
考查方向
解题思路
构造函数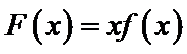
易错点
不能构造出新函数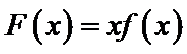
知识点
扫码查看完整答案与解析