- 函数奇偶性的性质
- 共128题
10.定义在








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.对于函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设函数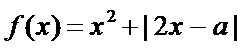
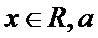
(1)若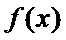
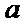
(2)设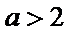
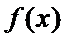
正确答案
(1)由已知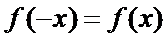
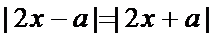
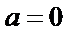
(2)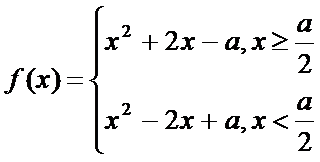
当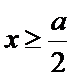
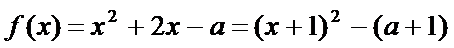
由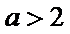
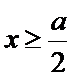
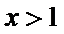
故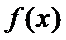
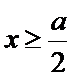
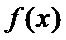
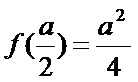
当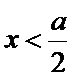
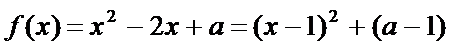
故当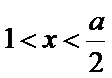
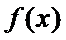
当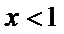
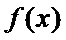
则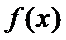
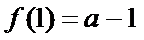
由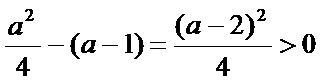
知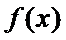
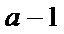
解析
解析已在路上飞奔,马上就到!
知识点
2.设函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.定义在R上的偶函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)求实常数
(2)设




正确答案
(1)
所以,当

(2)由


当
当



所以,
解析
解析已在路上飞奔,马上就到!
知识点
22.设

(1)当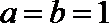

(2)设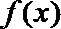


(3)当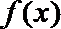
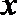

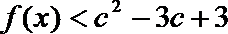
正确答案
(1)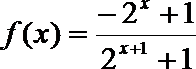

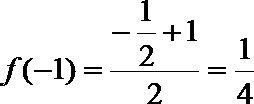
所以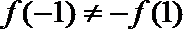
因此,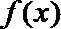
(2)
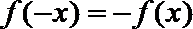
即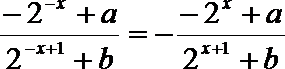
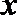
化简整理得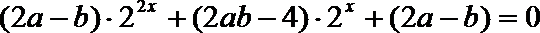
这是关于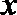

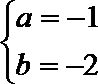
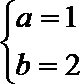
(3)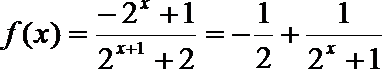
因为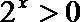
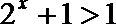
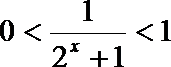

而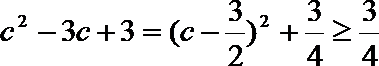
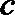
所以对任何实数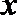
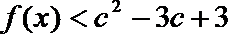
解析
解析已在路上飞奔,马上就到!
知识点
6.设奇函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析
























