- 函数奇偶性的性质
- 共128题
10．已知函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．设
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．已知函数
正确答案
-1
解析
解析已在路上飞奔，马上就到！
知识点
9． 若
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．定义在R上的函数
正确答案
-1
解析
解析已在路上飞奔，马上就到！
知识点
8．已知
值域为（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．
A 增函数且
B 减函数且
C 减函数且
D 增函数且
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．已知偶函数
A
B
C
D1
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17．已知f（x）为定义在[－1，1]上的奇函数，当x∈[－1，0]时，f（x）＝－（a∈R）．
（1）写出f（x）在[0，1]上的解析式；
（2）求f（x）在[0，1]上的最大值。
正确答案
（1）∵f（x）为定义在[－1，1]上的奇函数，
且f（x）在x＝0处有意义，
∴f（0）＝0，即f （0）＝
设x∈[0，1]，则－x∈[－1，0]．
∴f（－x）＝
又∵f（－x）＝－f（x）
∴－f（x）＝4x－2x．
∴f（x）＝2x－4x
（2）当x∈[0，1]，f（x）＝2x－4x＝2x－（2x）2，
∴设t＝2x（t>0），
则f（t）＝t－t2．
∵x∈[0，1]，
∴t∈[1，2]．
当t＝1时，取最大值，最大值为1－1＝0．
解析
解析已在路上飞奔，马上就到！
知识点
11． 已知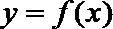
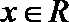
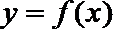
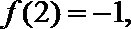
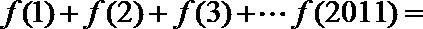
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析