- 函数奇偶性的性质
- 共128题
21.已知


(1)求
(2)是否存在实数a,使得当
正确答案
(1)设

故函数
(2)假设存在实数a,使得当

①当
由于



②当

综上所知,存在实数

解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数f(x)是定义在R上的偶函数,定义在R上的奇函数g(x)过点(-1,1),且g(x)=f(x-1),则f(7)+f(8)的值为______.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)若不等式



(2)在(1)的条件下, 当

(3)设




正确答案
(1)由已知不等式







(2) 则

当




(3) ∵

∵






∴

解析
解析已在路上飞奔,马上就到!
知识点
11.设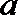
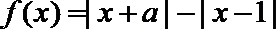
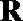
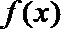
正确答案
[-1,1]
解析
解析已在路上飞奔,马上就到!
知识点
10.函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若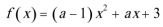
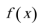
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知

正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.函数


①
②

③
④

其中正确命题的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析