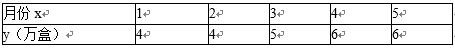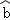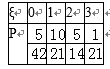- 相互独立事件的概率乘法公式
- 共42题
给出下列命题:
(1)已知事件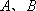
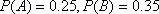
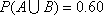
(2)已知事件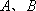
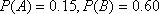
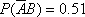
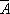
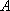
(3)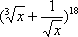
则其中真命题的序号是 [答]( )。
正确答案
解析
略
知识点
现将如图所示的5个小正方形涂上红、黄两种颜色,其中3个涂 红色,2个涂黄色,若恰有两个相邻的小正方形涂红色,则不同的涂法种数共有_________,(用数字作答)
正确答案
6
解析
略
知识点
(2x﹣1)5的展开式中x3项的系数是 ,(用数字作答)
正确答案
80
解析
在(2x﹣1)5的展开式中,通项公式为 Tr+1=

知识点
某同学在研究性学习中,收集到某制药厂今年前5个月甲胶囊生产产量(单位:万盒)的数据如下表所示:
(1)该同学为了求出y关于x的线性回归方程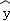
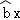
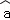
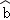
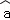
(2)若某药店现有该制药厂今年二月份生产的甲胶囊4盒和三月份生产的甲胶囊5盒,小红同学从中随机购买了3盒甲胶囊,后经了解发现该制药厂今年二月份生产的所有甲胶囊均存在质量问题,记小红同学所购买的3盒甲胶囊中存在质量问题的盒数为ξ,求ξ的分布列和数学期望。
正确答案
见解析。
解析
(1)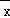
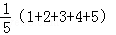
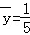
因线性回归方程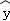
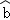
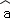
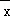
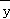
∴
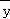
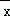
∴6月份的生产甲胶囊的产量数: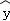
(2)ξ=0,1,2,3,
P(ξ=0)=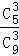
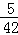
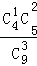
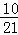
P(ξ=2)=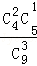
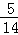
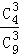
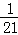
其分布列为
所以Eξ=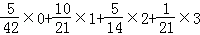
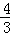
知识点
甲、乙、丙三名优秀的大学毕业生参加一所重点中学的招聘面试,面试合格者可以签约。甲表示只要面试合格就签约,乙与丙则约定,两个面试都合格就一同签约,否则两人都不签约。设每个人面试合格的概率都是P,且面试是否合格互不影响。已知至少有1人面试合格概率为
(1)求P。
(2)求签约人数
正确答案
见解析。
解析
解:
(1)至少1人面试合格概率为


(2)签约人数

甲不合格,乙丙至少一人不合格



签约人数为0的概率:





签约人数为2的概率:甲不合格,乙丙全部合格:

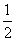
签约人数为3的概率:甲乙丙均合格:
分布表:
数学期望:
知识点
扫码查看完整答案与解析