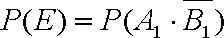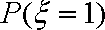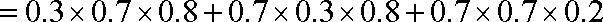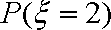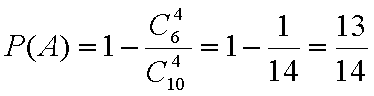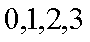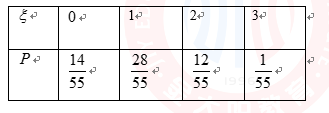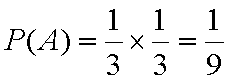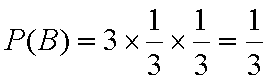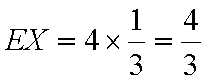- 相互独立事件的概率乘法公式
- 共42题
为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目的个数分别占总数的


(1)他们选择的项目所属类别互不相同的概率; 
(2)至少有1人选择的项目属于民生工程的概率.
正确答案
(1)
解析
解析: 记第



相互独立,
且
(1)他们选择的项目所属类别互不相同的概率
P=

(2)至少有1人选择的项目属于民生工程的概率 
P=
知识点
某校选拔若干名学生组建数学奥林匹克集训队,要求选拔过程分前后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔过程相互独立,根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三人合格的概率依次为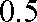



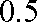
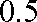
(1)求第一次选拔后甲、乙两人中只有甲合格,而乙不合格的概率;
(2)分别求出甲、乙、丙三人经过前后两次选拔后合格入选的概率;
(3)设经过前后两次选拔后合格入选的人数为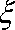
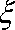
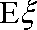
正确答案
见解析
解析
(1)分别设甲、乙经第一次选拔后合格为事件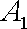
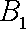
设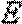
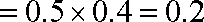
(2)分别设甲、乙、丙三人经过前后两次选拔后合格入选为事件A、B、C; 则:
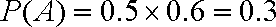
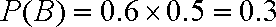
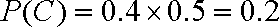
(3)经过前后两次选拔后合格入选的人数为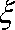
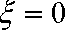
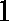
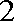

则,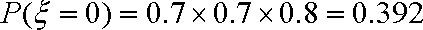
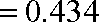
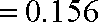
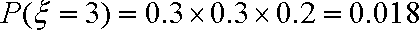
则,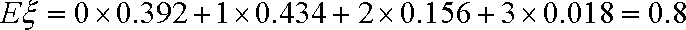
知识点
如图,已知椭圆










(1)求椭圆和双曲线的标准方程;
(2)设直线




(3)是否存在常数
恒成立

正确答案
见解析
解析
(1)由题意知,椭圆中,

又



所以椭圆的标准方程为
所以椭圆的焦点坐标为(

(2)设
因为点


因此
(3)由于


由韦达定理得
∴
同理可得
则
∴
故
即存在

知识点
某一部件由三个电子元件按如图所示方式连接而成,元件1或元件2正常工作,则部件正常工作:设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,

正确答案
解析
设该部件的使用寿命超过800小时的概率为P(A),因为三个元件的使用寿命均服从正态分布N(1000,σ2),所以元件1,2,3的使用寿命超过800小时的概率均为

知识点
某校选拔若干名学生组建数学奥林匹克集训队,要求选拔过程分前后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔过程相互独立,根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三人合格的概率依次为





(1)求第一次选拔后甲、乙两人中只有甲合格,而乙不合格的概率;
(2)分别求出甲、乙、丙三人经过前后两次选拔后合格入选的概率;
(3)设经过前后两次选拔后合格入选的人数为


正确答案
见解析
解析
(1)分别设甲、乙经第一次选拔后合格为事件

设

(2)分别设甲、乙、丙三人经过前后两次选拔后合格入选为事件A、B、C; 则:



(3)经过前后两次选拔后合格入选的人数为




则,



则,
知识点
把5名新兵分配到一、二、三3个不同的班,要求每班至少有一名且甲必须分配在一班,则所有不同的分配种数为 .
正确答案
50
解析
略
知识点
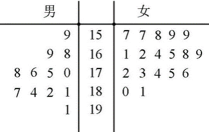
某单位为了提高员工素质,举办了一场跳绳比赛,其中男员工12人,女员工18人,其成绩编成如图所示的茎叶图(单位:分),分数在175分以上(含175分)者定为“运动健将”,并给予特别奖励,其他人员则给予“运动积极分子”称号.
(1)若用分层抽样的方法从“运动健将”和“运动积极分子”中抽取10人,然后再从这10人中选4人,求至少有1人是“运动健将”的概率;
(2)若从所有“运动健将”中选3名代表,用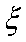
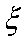
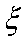
正确答案
见解析
解析
(1)根据茎叶图,有“运动健将”12人,“运动积极分子”18人
用分层抽样的方法,每个人被抽中的概率为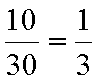
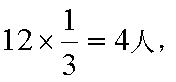
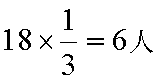
设事件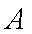
(2)由茎叶图知男“运动健将有”8人,女“运动健将”有4人,故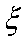
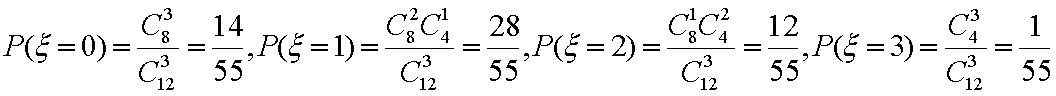

知识点
宿州市医疗保险实行定点医疗制度,按照“就近就医,方便管理”的原则,参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构。若甲、乙、丙、丁4名参加保险人员所在的地区附近有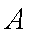

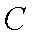
(1)求甲、乙两人都选择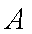
(2)求甲、乙两人不选择同一家社区医院的概率;
(3)设4名参加保险人员中选择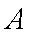

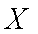
正确答案
见解析。
解析
(1)设“甲、乙两人都选择A社区医院”为事件A,那么
∴甲、乙两人都选择A社区医院概率为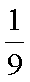
(2)设“甲、乙两人选择同一社区医院”为事件B,那么
∴甲、乙两人不选择同一社区医院的概率是
(3)依题意
∴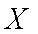
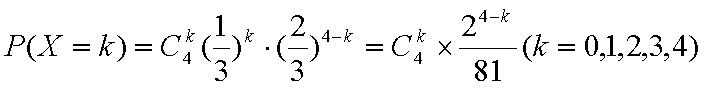
∴
知识点
18.某学校为了丰富学生的业余生活,以班级为单位组织学生开展古诗词背诵比赛,随机
抽取题目,背诵正确加10分,背诵错误减10分,只有“正确”和“错误”两种结果,
其中某班级的正确率为



(1) 求

(2)记

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为

(1)求甲乙二人中至少有一人破译出密码的概率;
(2)求
(3)设甲、乙、丙三人中破译出密码的人数为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析