- 相互独立事件的概率乘法公式
- 共42题
16.张师傅驾车从公司开往火车站,途径4个公交站,这四个公交站将公司到火车站分成5个路段,每个路段的驾车时间都是3分钟,如果遇到红灯要停留1分钟,假设他在各交通岗是否遇到红灯是相互独立的,并且概率都是
(1)求张师傅此行时间不少于16分钟的概率
(2)记张师傅此行所需时间为Y分钟,求Y的分布列和均值
正确答案
(1)
(2)记张师傅此行遇到红灯的次数为X,则


Y的均值为
解析
解析已在路上飞奔,马上就到!
知识点
18. 实验中学的三名学生甲、乙、丙参加某大学的自主招生考核测试,在本次考核中只有合格和优秀两个等次,若考核为合格,则授予10分降分资格;考核为优秀,授予20分降分资格。假设甲、乙、丙考核为优秀的概率分别为


(1)求在这次考核中,甲、乙、丙三名同学中至少有一名考核为优秀的概率;
(2)记在这次考核中甲、乙、丙三名同学所得的降分之和为随机变量
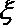
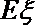
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 甲、乙两班参加数学知识竞赛,每班出3人组成代表队,每人一道必答题,答对为本队得1分,答错或不答得0分,假如甲队每人答对的概率均为




(Ⅰ)求随机变量

(Ⅱ)用A表示事件“甲、乙两队得分和为3”,B表示事件“甲队得分大于乙队得分”,求P(AB)
正确答案
解:(Ⅰ)
而P(






因而

(Ⅱ)P(AB)=
解析
解析已在路上飞奔,马上就到!
知识点
18. 甲乙两班进行消防安全知识竞赛,每班出3人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得1分,答错或不答都得0分,已知甲队3人每人答对的概率分别为


(1)求随机变量

(2)求在甲队和乙队得分之和为4的条件下,甲队比乙队得分高的概率。
正确答案
(1)




解析
解析已在路上飞奔,马上就到!
知识点
18.质点A位于数轴x=0处,质点B位于x=2处.这两个质点每隔1秒钟都向左或向右平移一个单位,设向左移动的概率为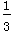
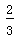
(1)求3秒后,质点A在点x=1处的概率;
(2)求2秒后,质点A、B同时在x=2处的概率。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.现有A,B两球队进行友谊比赛,设A队在每局比赛中获胜的概率都是
(Ⅰ)若比赛6局,求A队至多获胜4局的概率;
(Ⅱ)若采用“五局三胜”制,求比赛局数ξ的分布列和数学期望.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某班共有24人参加同时开设的数学兴趣小组和物理兴趣小组,其中参加数学兴趣小组的有6名女生,10名男生;参加物理兴趣小组的有3名女生,5名男生,现采用分层抽样方法从两组中抽取3人。
(1)求抽取的3人中恰有一名女生来自数学兴趣小组的概率;
(2)记X表示抽取3人中男生的人数,求X的分布列和数学期望。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.为了倡导健康、低碳、绿色的生活理念,某市建立了公共自行车服务系统鼓励
市民租用公共自行车出行,公共自行车按每车每次的租用时间进行收费,具体收费标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,收费1元;
③租用时间为2小时以上且不超过3小时,收费2元;
④租用时间超过3小时的时段,按每小时2元收费(不足1小时的部分按1小时计算)
已知甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0. 4和0. 5 ;租用时间为1小时以上且不超过2小时的概率分别是0.5和0.3.
(I)求甲、乙两人所付租车费相同的概率;
(II)设甲、乙两人所付租车费之和为随机变量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在汶川大地震后对唐家山堰塞湖的抢险过程中,武警官兵准备用射击的方法引爆从湖坝上游漂流而下的一个巨大的汽油罐.已知只有5发子弹,第一次命中只能使汽油流出,第二次命中才能引爆.每次射击是相互独立的,且命中的概率都是
(1)求油罐被引爆的概率;
(2)如果引爆或子弹打光则停止射击,设射击次数为ξ.求ξ的分布列及数学期望E(ξ).(结果用最简分数表示)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是
(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(Ⅱ)求这名学生在上学路上因遇到红灯停留的总时间
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析



















