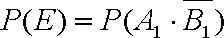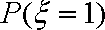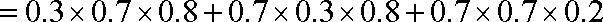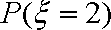- 相互独立事件的概率乘法公式
- 共42题
为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目的个数分别占总数的


(1)他们选择的项目所属类别互不相同的概率; 
(2)至少有1人选择的项目属于民生工程的概率.
正确答案
(1)
解析
解析: 记第



相互独立,
且
(1)他们选择的项目所属类别互不相同的概率
P=

(2)至少有1人选择的项目属于民生工程的概率 
P=
知识点
某校选拔若干名学生组建数学奥林匹克集训队,要求选拔过程分前后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔过程相互独立,根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三人合格的概率依次为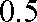



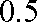
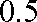
(1)求第一次选拔后甲、乙两人中只有甲合格,而乙不合格的概率;
(2)分别求出甲、乙、丙三人经过前后两次选拔后合格入选的概率;
(3)设经过前后两次选拔后合格入选的人数为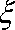
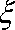
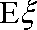
正确答案
见解析
解析
(1)分别设甲、乙经第一次选拔后合格为事件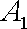
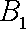
设
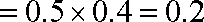
(2)分别设甲、乙、丙三人经过前后两次选拔后合格入选为事件A、B、C; 则:
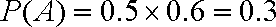
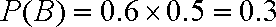
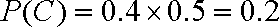
(3)经过前后两次选拔后合格入选的人数为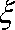
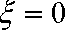
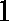

则,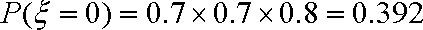
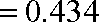
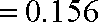
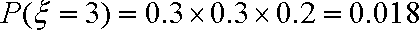
则,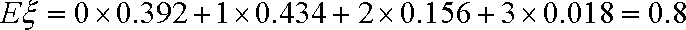
知识点
如图,已知椭圆










(1)求椭圆和双曲线的标准方程;
(2)设直线




(3)是否存在常数
恒成立

正确答案
见解析
解析
(1)由题意知,椭圆中,

又



所以椭圆的标准方程为
所以椭圆的焦点坐标为(

(2)设
因为点


因此
(3)由于


由韦达定理得
∴
同理可得
则
∴
故
即存在

知识点
某校选拔若干名学生组建数学奥林匹克集训队,要求选拔过程分前后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔过程相互独立,根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三人合格的概率依次为





(1)求第一次选拔后甲、乙两人中只有甲合格,而乙不合格的概率;
(2)分别求出甲、乙、丙三人经过前后两次选拔后合格入选的概率;
(3)设经过前后两次选拔后合格入选的人数为


正确答案
见解析
解析
(1)分别设甲、乙经第一次选拔后合格为事件

设

(2)分别设甲、乙、丙三人经过前后两次选拔后合格入选为事件A、B、C; 则:



(3)经过前后两次选拔后合格入选的人数为




则,



则,
知识点
把5名新兵分配到一、二、三3个不同的班,要求每班至少有一名且甲必须分配在一班,则所有不同的分配种数为 .
正确答案
50
解析
略
知识点
扫码查看完整答案与解析