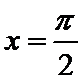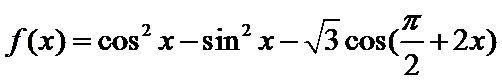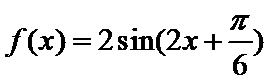正弦函数的单调性
共119题

· 正弦函数的单调性

正弦函数的单调性
共119题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

7．定义矩阵，若，则（）

A图象关于中心对称

B图象关于直线对称

C在区间上单调递增

D周期为的奇函数

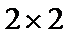
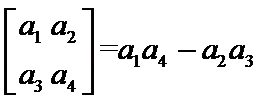
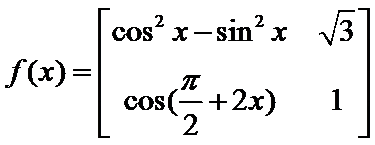
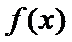
正确答案

解析

根据矩阵的定义，可以得到

所以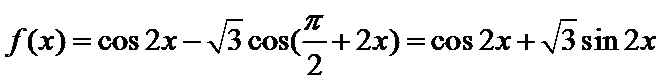，所以

根据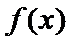的性质判断性质，所以选C

考查方向

三角函数

解题思路

先根据矩阵的定义，得到f(x)的解析式，然后根据函数的解析式判断函数的相关性质.

易错点

三角函数公式记忆混淆

知识点

三角函数的周期性及其求法正弦函数的奇偶性正弦函数的单调性正弦函数的对称性

题型：单选题

单选题 · 5 分

6.已知是函数的一个极大值点，则的一个单调递减区间是

正确答案

解析

由是函数的一个极大值点得，所以，得，所以，令，得，所以的单调递减区间是，故选B。

考查方向

本题主要考查了三角函数最值和单调区间的求法,属于比较简单问题，在各类试卷中出现的频率较高。

解题思路

1、先由是函数的一个极大值点求出；

2、然后求函数的单调递减区间，最后令即可得到答案。

易错点

1、将三角函数的最值以极值的形式出现导致无法理解题意致误。

2、将三角函数的最值、单调区间记错、求错出错。

知识点

正弦函数的单调性三角函数的最值

题型：单选题

单选题 · 5 分

8.设函数的图象在时取最大值，它的周期是，则（）

B在区间上是减函数

D的最大值是A；

正确答案

解析

由题得周期为，得，,时单调递减

考查方向

本题主要考察了三角函数的图像，平移，周期，最值，对称轴和对称中心难度系数不高，

解题思路

该题首先根据周期求出，在根据对称轴的最大值得出，最后找到该三角函数的单调性

易错点

本题易错在（１）忽略Ａ为负值（２）对称中心计算错误（３）单调性不能判断

知识点

正弦函数的图象正弦函数的单调性正弦函数的对称性三角函数的最值

题型：简答题

简答题 · 12 分

16.已知函数（其中），若的一条对称轴离最近的对称中心的距离为

（I）求的单调递增区间；

（II）在中角A、B、C的对边分别是满足恰是的最大值，试判断的形状.

正确答案

解：(Ⅰ)因为

的对称轴离最近的对称中心的距离为

所以，所以，所以

解

得：

所以函数单调增区间为

(Ⅱ) 因为，由正弦定理，

得

因为

，所以

所以，所以

所以

根据正弦函数的图象可以看出，无最小值,有最大值，

此时，即,所以

所以为等边三角形

解析

见答案

考查方向

本题主要考查正弦定理和余弦定理的性质，属于基础题

解题思路

根据题意换成三角函数一般形式，然后根据函数最值判断，第二问求出ABC角度的大小进而判定三角形形状。

易错点

混淆两个定理的性质

知识点

正弦函数的单调性三角函数中的恒等变换应用正弦定理的应用

题型：单选题

单选题 · 5 分

6.函数f(x)＝(ω>0)在区间上单调递增，在区间上单调递减，则ω为(　　)

正确答案

解析

由题意可知函数在x=时取得最大值，就是

所以，只有k=0时，ω=2满足选项，故选项为B

考查方向

本题考查了函数的图象及单调性，最值等性质。

解题思路

利用函数图象的单调性等性质，得出函数在x=时取得最大值这一隐含条件，求出答案。

易错点

看不出函数在x=时取得最大值这一隐含条件，从而不能快速得到答案。

知识点

正弦函数的单调性

继续学习学习下一知识点

下一知识点 : 正弦函数的对称性

百度题库 > 高考 > 理科数学 > 正弦函数的单调性

扫码查看完整答案与解析