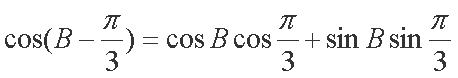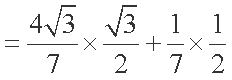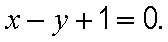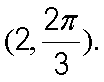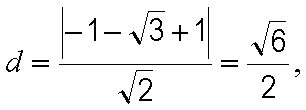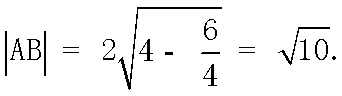- 正弦函数的单调性
- 共119题
已知偶函数f(x)(x≠0)在区间(0,+∞)上(严格)单调,则满足f(x2﹣2x﹣1)=f(x+1)的所有x的和为( )
正确答案
解析
解:由题意得,x2﹣2x﹣1=x+1,或(x2﹣2x﹣1)+(x+1)=0,即x2﹣3x﹣2=0,①或x2﹣x=0.②
设方程①两根为x1,x2,方程②的根为x3,x4,则x1+x2=3,x3+x4=1,
所以满足要求的所有x的和为:x1+x2+x3+x4=4。
故选D
知识点
在
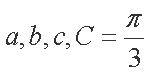
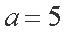
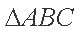
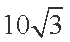
(1)求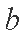

(2)求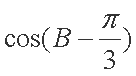
正确答案
见解析
解析
解析:(1)由已知,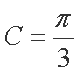
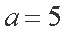
因为 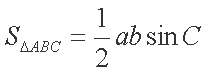
即 
解得 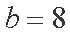
由余弦定理可得
所以 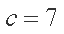
(2)由(1)有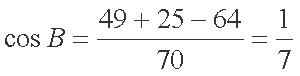
由于B是三角形的内角,
易知 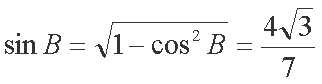
所以

知识点
已知在



(1)求角A、B、C的大小;
(2)设函数

正确答案
(1)

解析
解析:(1)由题设及正弦定理知:
∴


当




当


∴

(2) 由(1)及题设知:
当

即

它的相邻两对称轴间的距离为 
知识点
在直角坐标系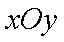
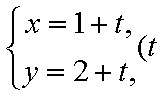
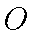
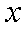
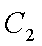
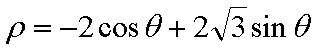
(1)求直线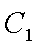
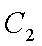
(2)设直线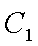
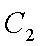
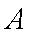
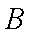
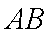
正确答案
见解析
解析
解析:
(1)由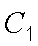
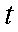
圆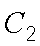
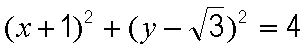
所以圆心的直角坐标为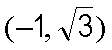
所以圆心的一个极坐标为
(2)由(1)知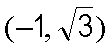

所以
知识点
已知函数
(1)求函数

(2)求函数
正确答案
见解析。
解析
(1)
令 
函数


(2) 由
得: 
故
知识点
扫码查看完整答案与解析