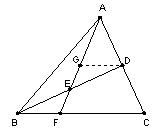- 空间点、线、面的位置关系
- 共375题
正确答案
见解析
解析
分别以



则
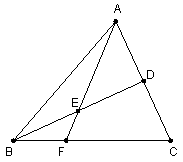
(1) 证明方法一::







方法二:易证



(2)方法一:设




则















方法二:
设



令
可求得平面

要







(3)可求得平面



知识点
如图,在△
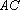
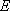
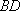
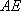
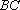
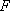
(1)求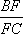
(2)若△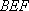
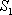
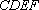
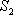
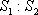
正确答案
见解析。
解析
(1)过D点作DG∥BC,并交AF于G点,∵E是BD的中点,∴BE=DE,
又∵∠EBF=∠EDG,∠BEF=∠DEG,∴△BEF≌△DEG,则BF=DG,
∴BF:FC=DG:FC,又∵D是AC的中点,则DG:FC=1:2,
则BF:FC=1:2;即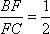
(2)若△BEF以BF为底,△BDC以BC为底,则由(1)知BF:BC=1:3,又由BE:BD=1:2可知
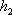
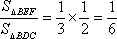
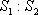
知识点
如图所示,三棱锥









正确答案
见解析
解析
(方法一):取








因为














设


在




在
∴ 异面直线


(方法二):以
















设









设异面直线






∴ 异面直线


知识点
如图,已知
(1)证明:平面
(2)当二面角

正确答案
见解析。
解析
(1)




又
(2)方法一:
建立如图所示的空间直角坐标系,设







假设平面





同理可以求得:

此时,正四棱柱
四棱锥
方法二:
过点



容易证得

所以

所以






即
所以
此时,正四棱柱
四棱锥
知识点
如图6,四棱柱








(1)证明:平面

(2)若

所成角的余弦值。
正确答案
见解析。
解析
(1)依题意,

















(2)取












,所以
(方法二)以













(1)设平面

,








(2)由




所以异面直线

知识点
如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD是边长为2的等边三角形,且与底面ABCD垂直,E为PA的中点。
(1)求证:DE∥平面PBC;
(2)求二面角
正确答案
见解析。
解析
(1)
法一 如图,取AB的中点F,连接DF,EF。
在直角梯形ABCD中,CD∥AB,且AB=4,CD=2,所以
所以四边形BCDF为平行四边形,所以DF∥BC,(2分)
在△PAB中,PE=EA,AF=FB,所以EF//PB。
又因为DF

因为DE
法二
取PB的中点M,连接CM,ME。
在△PAB中,PE=EA,PM=MB,所以
在直角梯形ABCD中,CD∥AB,且AB=4,CD=2,
故

所以四边形CDEM为平行四边形,故DE∥CM。
因为CM

所以DE∥平面PBC,(4分)
(2)取AD的中点O,BC的中点N,连接ON,则ON∥AB。
在△PAD中,PA=PD=AD=2,所以PO⊥AD,
又因为平面PAD⊥平面ABCD,平面PAD
所以PO⊥平面ABCD,(6分)
如图,以O为坐标原点;分别以OA,ON,OP所在直线为





因为E为PA的中点,所以


因为平面PAD⊥平面ABCD,平面PAD
所以PO⊥平面ABD,故
设平面EBD的法向量为
由


令



所以
设二面角



知识点
如图,四棱锥

(1)求二面角
(2)求四棱锥

正确答案
见解析
解析
(1)方法一:如图(1)连结AC、BD交于菱形的中心O,过O
作OG⊥AF,G为垂足. 连结BG、DG.
由BD⊥AC,BD⊥CF,得BD⊥平面ACF, 故BD⊥AF. 于是AF⊥平面BGD,
所以BG⊥AF,DG⊥AF,∠BGD为二面角B-AF-D的平面角. …………………3分
由FC⊥AC,FC=AC=2,得∠FAC

由OB⊥OG,OB=OD=

即二面角B-AF-D的大小为
方法二:设AC与BD交点为O,以O为坐标原点,分别以BD 、AC所在直线为x轴
y轴建立如图所示的空间直角坐标系
则A(0,-1,0),B(




设平面ABF,平面ADF的法向量分别为
设
由
令
同理可得

∴二面角B-AF-D的大小为
(2)如图(2)连EB、EC、ED,设直线AF与直线CE相交于点H,
则四棱锥E-ABCD与四棱锥F-ABCD的公共部分为四棱锥H-ABCD.
过H作HP⊥平面ABCD,所以平面ACFE⊥平面ABCD,
从而
由

又因为
故四棱锥

知识点
如图,矩形













(1)证明:MN∥平面
(2)若二面角

正确答案
见解析
解析
解析:(1)证:连结DB1 、DC1 ∵四边形DBB1D1为矩形,M为D1B的中点 ……2分
∴M是DB1与D1B的交点,且M为DB1的中点
∴MN∥DC1,∴MN∥平面DD1C1C ……………4分
(2)解:四边形

且BB1∥CC1∥

∴∠BDC = 90° ……………6分

D(0,0,0),B(2,0,0),C(0,2,0),D1(0,0,


点M、N分别为D1B和B1C1的中点,∴
设平面D1MN的法向量为m = (x,y,z),则

令x = 1得:
即
设平面MNC的法向量为n = (x,y,z),则

即
∵二面角D1-MN-C为直二面角 ∴m⊥n,故
∴二面角D1-MN-C为直二面角时,
知识点
函数


正确答案
解析
∵











知识点
甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,

正确答案
解析
由题意可知





知识点
扫码查看完整答案与解析