- 空间点、线、面的位置关系
- 共375题
如图2，三角形
21.证明：
22.求二面角
23.求直线
正确答案
（1）见解析；
解析
（1）证明：∵ 
∴ 
∴ 
∴ 
考查方向
解题思路
第一问，利用面面垂直的性质定理，可得
易错点
定理的应用不熟练以及建系求角过程中，计算错误。
正确答案
解析
（2）∵ 
∴ 
∴ 
∴ 
∴ 
在
∴ 
考查方向
解题思路
第一问，利用面面垂直的性质定理，可得
易错点
定理的应用不熟练以及建系求角过程中，计算错误。
正确答案
解析
（3）如下图所示，连接
∵ 
∴ 
∴ 
在
由余弦定理可得
∴ 直线
考查方向
解题思路
第一问，利用面面垂直的性质定理，可得
易错点
定理的应用不熟练以及建系求角过程中，计算错误。
如图4，直三棱柱ABC-A
20.证明：平面AEF⊥平面B
21.若直线A
正确答案
如图，因为三棱柱
所以
所以
解析
见答案
考查方向
解题思路
先证明
易错点
不会证明
正确答案
解析
设AB的中点为D，连接
由题设知，
所以，
在
故三棱锥F-AEC的体积
考查方向
解题思路
设AB的中点为D，证明
由题设知，
易错点
找不到直线与平面所成的角；
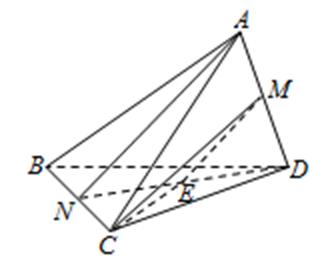
13.如图，三棱锥A-BCD中，AB＝AC＝BD＝CD＝3，AD＝BC＝2，点M,N分别是AD,BC的中点，则异面直线AN，CM所成的角的余弦值是 ．
正确答案
解析
试题分析：利用中位线作出异面直线所成的角，然后在三角形中利用余弦定理求出余弦值即可。
连结ND，取ND 的中点为E，连结ME，则ME∥AN，异面直线AN，CM所成的角就是∠EMC，
∵
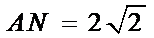
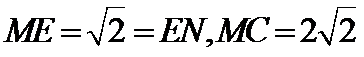
又∵EN⊥NC，∴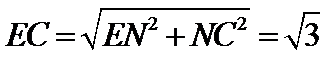
∴
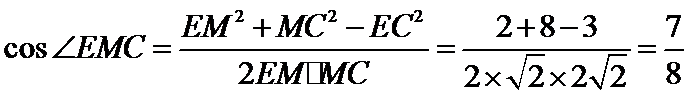
故答案为：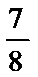
考查方向
解题思路
连结ND，取ND 的中点为E，连结ME说明异面直线AN，CM所成的角
就是∠EMC通过解三角形，求解即可．
易错点
异面直线所成的角为锐角或直角.
知识点
14.如图，四边形ABCD和ADPQ均为正方形，它们所在的平面互相垂直，动点M在线段PQ上，E、F分别为AB、BC的中点。设异面直线EM与AF所成的角为
正确答案
解析
建立坐标系如图所示.设
考查方向
解题思路
建立坐标系后直接根据坐标求解即可；
易错点
1.点或向量的坐标写错；
不会利用基本不等式求最值。
知识点
5.已知异面直线
A不存在一个平面
B存在一个平面
C不存在一个平面
D存在一个平面
正确答案
解析
A. 符合异面直线定义,正确 ;B. 举出特例, 如图，正确；
C．正确，假设存在平面
考查方向
解题思路
根据题中的叙述条件画出图形, 结合定理.公理.性质进行论证.
易错点
对定理和性质掌握不准易出错
知识点
16．如图，在凸四边形
正确答案
解析
在三角形BCD中，
因为角ABC在
所以
所以BD的最大值为
考查方向
解三角形，余弦定理
解题思路
将BD用含有已知线段长，角度表示出来，然后化简变换，求出最值。
易错点
化简错误，计算错误
教师点评
求最值之类的问题，一般都是先用其他已知条件表示出来，然后利用三角函数或者不等式的性质判断出得到最值的情况。
知识点
如图13，四棱锥PABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点。
正确答案
见解析。
解析
(1)证明：连接BD交AC于点O，连接EO.
因为ABCD为矩形，所以O为BD的中点。
又E为PD的中点，所以EO∥PB.
因为EO⊂平面AEC，PB⊄平面AEC，
所以PB∥平面AEC.
(2)
因为PA⊥平面ABCD，ABCD为矩形，
所以AB，AD，AP两两垂直。
知识点
如图，四棱锥S﹣ABCD的底面为正方形，SD⊥底面ABCD，则下列结论中不正确的是（ ）
A
B
C
D
正确答案
解析
∵SD⊥底面ABCD，底面ABCD为正方形，
∴连接BD，则BD⊥AC，根据三垂线定理，可得AC⊥SB，故A正确；
∵AB∥CD，AB⊄平面SCD，CD⊂平面SCD，
∴AB∥平面SCD，故B正确；
∵SD⊥底面ABCD，
∠SAD是SA与平面SBD所成的角，∠SCD是SC与平面SBD所成的角，
而△SAD≌△SBD，
∴∠SAD=∠SCD，即SA与平面SBD所成的角等于SC与平面SBD所成的角，故C正确；
∵AB∥CD，∴AB与SC所成的角是∠SCD，DC与SA所成的角是∠SAB，
而这两个角显然不相等，故D不正确；
故选D。
知识点
16.如图，在直三棱柱
求证：（1）
（2）
正确答案
证明：（1）由题意知，
又
又因为
所以
（2）因为棱柱
所以
因为
又因为
所以
又因为
因为
因为
又因为
解析
解析已在路上飞奔，马上就到！
知识点
6. 在长方体
所成角的大小为
正确答案
解析
因为
考查方向
解题思路
异面直线所成的角要通过平移找到所求的角。
易错点
寻找异面直线所成的角要找对。
知识点
扫码查看完整答案与解析