- 空间点、线、面的位置关系
- 共375题
某象棋比赛规则如下:两名选手比赛时,每局胜者得1分,负者得




(1)求比赛进行

(2)设

正确答案
(1)
解析
(1)比赛进行

则所求概率为
(2)由题意知,

则
故
………10分
则
知识点
已知公比不为





(1)求等比数列
(2)对









正确答案
见解析
解析
(1)因为
所以
即



所以等比数列

(2)

知识点
如图5,已知△ABC为直角三角形,∠ACB为直角.以AC为直径作半圆O,使半圆O所在平面⊥平面ABC,P为半圆周异于A,C的任意一点。
(1) 证明:AP⊥平面PBC
(2) 若PA=1,AC=BC=2,半圆O的弦PQ∥AC,求平面PAB与平面QCB所成锐二面角的余弦值。
正确答案
见解析。
解析

知识点
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
(1)求证:A1C⊥平面BCDE;
(2)若M是A1D的中点,求CM与平面A1BE所成角的大小;
(3)线段BC上是否存在点P,使平面A1DP与平面A1BE垂直?说明理由
正确答案
见解析
解析




又

又


(2)如图建系



∴
设平面
则

∴
又∵
∴
∴
∴


(3)设线段



则
设平面

则
∴
假设平面

则



∵




知识点
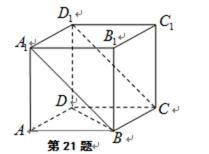
如图,正方体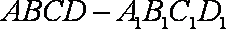
(1)求直线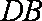
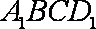
(2)求四棱锥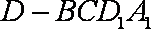
正确答案
(1)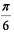
解析
解析:(1)以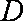
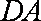
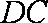
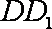
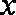
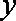
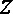
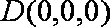
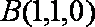
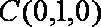
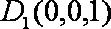
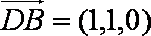
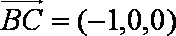

设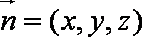
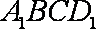
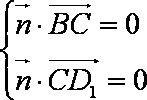
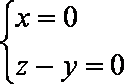
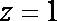
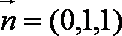
设直线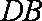
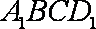
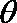
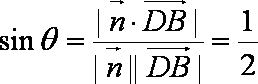
由于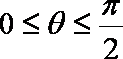
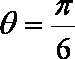
即直线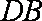
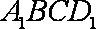
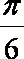
(2)由(1)得
所以点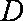
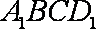
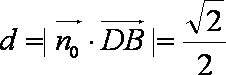
因为四边形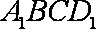
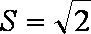
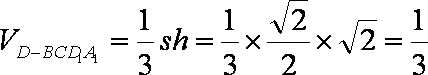
知识点
如右图,在△





正确答案
解析
略
知识点
一个几何体的三视图如图所示,该几何体的表面积是___________。
正确答案
解析
略
知识点
如图,在直三棱柱


(1)求四棱锥
(2)求异面直线AE与A1C所成的角。
正确答案
见解析
解析
(1)四棱锥


∴
(2)取B1C1的中点E1,连A1E1,E1C,
则AE∥A1E1,∴∠E1A1C是异面直线AE与A1C所成的角。…(8分)
由






所以异面直线AE与A1C所成的角为
知识点
如图,在直三棱柱






(1)求四棱锥
(2)求


正确答案
(1)4(2)
解析
解析:(1)
(2)建立如图所示的直角坐标系,则






设平面


所以
平面

所以



知识点
如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,



(1)求五棱锥
(2)求平面

正确答案
见解析
解析
(1)连接



得



所以



过点




则

因为正方形


得到:

所以
所以五棱锥

(2)由(1)知道




如图以点






设平面



令

设平面



令


所以



知识点
扫码查看完整答案与解析