空间点、线、面的位置关系
共375题

空间点、线、面的位置关系
共375题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

1．已知集合等于（）

A{2，3}

B{1，2，3}

C{1，－1，2，3}

D{2，3，x，y}

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面的基本性质及推论

题型：单选题

单选题 · 4 分

16．已知函数，在同一坐标系中，y=f -1（x）与y=的图象可能是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面的基本性质及推论

题型：单选题

单选题 · 5 分

8.已知正方体的棱长为2, 长为2的线段的一个端点在棱上运动, 另一端点在正方形内运动, 则的中点的轨迹的面积为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面的基本性质及推论

题型：填空题

填空题 · 4 分

15．如图所示，过抛物线的焦点F作直线交C于A、B两点，过A、B分别向C的准线作垂线，垂足为，已知四边形的面积分别为15和7，则的面积为。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面的基本性质及推论

题型：单选题

单选题 · 5 分

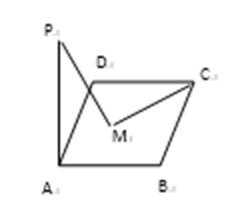
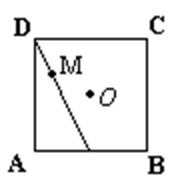
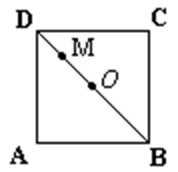
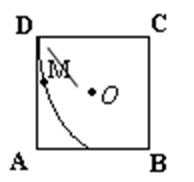
11．如图△ADP为正三角形，四边形ABCD为正方形，平面PAD⊥平面ABCD，M为平面ABCD内的一动点，且满足MP=MC．则点M在正方形ABCD内的轨迹为（O为正方形ABCD的中心）( )

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面的基本性质及推论平面与平面垂直的判定与性质

题型：单选题

单选题 · 5 分

设是两条不同的直线，是三个不同的平面，下列命题正确的是（　）

正确答案

解析

略

知识点

平面的基本性质及推论

题型：单选题

单选题 · 5 分

如图，是圆的直径，是圆上的点，，，，则的值为

正确答案

解析

设，建立如图所示坐标系，则，

，，故。

知识点

平面的基本性质及推论

题型：简答题

简答题 · 12 分

如图，在斜三棱柱中，点、分别是、的中点，平面.已知，.

（1）证明：平面；

（2）求异面直线与所成的角；

（3）求与平面所成角的正弦值。

正确答案

见解析。

解析

解法一：

（1）证明：∵点、分别是、的中点，

∴ ，又∵平面，平面，

∴平面。

（2）∵平面，∴，又∵，且，

∴平面,∴。

又∵， ∴四边形为菱形，

∴，且∴平面,

∴，即异面直线与所成的角为。

（3）设点到平面的距离为，∵，

即△。

又∵在△中，,∴△。

∴，∴与平面所成角的正弦值。

解法二：

如图建系，，

，

。

（1）∵，，∴，即，

又∵平面，平面，∴平面。

（2）∵，，∴，即∴，

∴异面直线与所成的角为。

（3）设与平面所成角为，∵，

设平面的一个法向量是

则即

不妨令，可得，

∴，

∴与平面所成角的正弦值。

知识点

平面的基本性质及推论

题型：填空题

填空题 · 5 分

13．设双曲线的渐近线与抛物线相切，则该双曲线的离心率等于__________ 。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面的基本性质及推论

题型：填空题

填空题 · 5 分

11．如图，在直角梯形中，已知，，，，，若为的中点，则的值为___________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面的基本性质及推论

继续学习学习下一知识点

下一知识点 : 直线、平面平行的判定与性质

百度题库 > 高考 > 理科数学 > 空间点、线、面的位置关系

扫码查看完整答案与解析