空间点、线、面的位置关系
共375题

空间点、线、面的位置关系
共375题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 16 分

19.若函数为定义域上单调函数，且存在区间（其中），使得当时，的取值范围恰为，则称函数是上的正函数，区间叫做等域区间。

（1）已知是上的正函数，求的等域区间；

（2）试探究是否存在实数，使得函数是上的正函数？若存在，请求出实数的取值范围；若不存在，请说明理由。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平行公理

题型：简答题

简答题 · 12 分

20．在平面直角坐标系中，已知抛物线，过定点作直线交该抛物线于M．N两点．

（I）求弦长的最小值；

（II）是否存在平行于y轴的直线l，使得l被以AM为直径的圆所截得的弦长为定值？若存在，求出l的方程；若不存在，说明理由．

正确答案

解：（I）设，

直线

①当时，

②当时，联立与

得

比较①②知

（II）设存在平行于y轴的直线l，方程为，，圆心为

l被圆C截得的弦长为q，则由圆的几何性质可得：

当时，为定值

故存在这样的直线l，其方程为

解析

解析已在路上飞奔，马上就到！

知识点

平行公理

题型：简答题

简答题 · 12 分

17．在中，角、、的对边分别为、、，。

（1）求角的值；

（2）若，，求的面积。

正确答案

解：

（1）

。

（2）由

。

解析

解析已在路上飞奔，马上就到！

知识点

平行公理

题型：单选题

单选题 · 5 分

5.正方形ABCD在平面α内,PB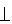α,则PD与对角线AC的位置关系是（　　）.

A平行

B相交但不垂直

C相交垂直

D异面垂直

正确答案

解析

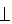
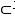
∵PB平面α,∴PB⊥AC.又在正方形ABCD中,ACBD,∴AC平面PBD.又PD平面PBD,∴ACPD.显然PD与AC异面,故PD与AC异面垂直.

知识点

平行公理

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：填空题

填空题 · 5 分

在平面直角坐标系中，若直线 (t为参数) 过椭圆 (　为参数) 的右顶点，则常数 .

正确答案

解析

略

知识点

空间图形的公理

题型：填空题

填空题 · 4 分

将外形和质地一样的4个红球和6个白球放入同一个袋中，将它们充分混合后，现从中取出4个球，取出一个红球记2分，取出一个白球记1分，若取出4个球总分不少于5分，则有________种不同的取法。

正确答案

195

解析

略

知识点

空间图形的公理

题型：简答题

简答题 · 14 分

如图，为圆柱的母线，

是底面圆的直径，分别是的中点，.

（1）证明:;

（2）求四棱锥与圆柱的体积比;

(3)若,求与面所成角的正弦值。

正确答案

见解析。

解析

知识点

空间图形的公理

题型：简答题

简答题 · 12 分

设△的内角所对的边分别为,且,.

（1）求的值;

（2）求的值.

正确答案

见解析。

解析

（1）由余弦定理,得,

又,,,所以,解得,.

（2）在△中,,

由正弦定理得 ,

因为,所以为锐角,所以

因此 .

知识点

空间图形的公理

继续学习学习下一知识点

下一知识点 : 直线、平面平行的判定与性质

百度题库 > 高考 > 理科数学 > 空间点、线、面的位置关系

扫码查看完整答案与解析