等差数列_章节学习

1

题型：填空题

|

填空题 · 5 分

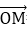
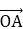
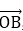
8.已知等差数列{an}的前n项和为Sn,若=a2015+a2016,且A,B,M三点共线（该直线不过点O）,则S4030=_______.

正确答案

2015

解析

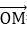
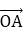
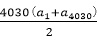
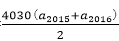
若O,A,B,M为平面内四点,则A,B,M三点在一条直线上,当且仅当存在一对实数m,n,使=m+n,且m+n=1,所以a2015+a2016=1,故S4030===2015

知识点

向量的共线定理等差数列的基本运算等差数列的性质及应用等差数列的前n项和及其最值

1

题型：填空题

|

填空题 · 5 分

9.设F是椭圆的右焦点,且椭圆上至少有11个不同的点Pi(i=1,2,3,…),使,…组成公差为d的等差数列,则d的取值范围为　　　　.

正确答案

解析

若公差d>0,则|FP1|最小,

,数列中的最大项为

并设为第n项,

则

注意到d>0,得

若d<0,易得

那么d的取值范围为

知识点

等差数列的基本运算等差数列的性质及应用数列与解析几何的综合椭圆的几何性质

1

题型：单选题

|

单选题 · 5 分

4.对大于1的自然数m的三次幂可用奇数进行以下方式的“分裂”,233343…仿此,若2015会在m3的“分裂”数中,则m的值为（　　）.

A44

B45

C46

D47

正确答案

B

解析

由题意知,自然数m的三次幂可用m个连续奇数进行“分裂”,把1算在内,从13到m3用从1开始的连续奇数共有1+2+3+…+m=,2015是从1开始的1008个奇数,解<1008≤,解得m=45.

知识点

等差数列的基本运算等差数列的性质及应用进行简单的合情推理

1

题型：单选题

|

单选题 · 5 分

7.在等差数列{an}中，，则数列前9项之和S9等于（）

A24

B48

C72

D108

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的性质及应用等差数列的前n项和及其最值

1

题型：填空题

|

填空题 · 5 分

12.已知数列{an}中a1=1，其前n项和为Sn，且点P（an，an+1）在直线 l：x-y+1=0上，则S10=__________。

正确答案

55

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的判断与证明等差数列的前n项和及其最值数列与解析几何的综合

1

题型：简答题

|

简答题 · 13 分

17.设等差数列{an}满足a3=5,a10=-9。

（1）求{an}的通项公式；

（2）求数列{an}的前n项和Sn及使得Sn最大的序号n的值。

正确答案

（1）由得

解得

∴

（2）由（1）知，

∴当n = 5时，Sn取得最大

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项等差数列的基本运算等差数列的性质及应用等差数列的前n项和及其最值

1

题型：填空题

|

填空题 · 5 分

14.已知数列的前n项和Sn=10n-n2(n∈N+),则数列的前n项和Tn为　　　　.

正确答案

解析

当n=1时,a1=S1=9；当n≥2时,an=Sn-Sn-1=11-2n,

由于n=1时,a1=9也满足11-2n,

因此an=11-2n.

(1)当n>5时,

(2)当n≤5时,

综合(1)(2),得

知识点

等差数列的基本运算等差数列的性质及应用等差数列的前n项和及其最值分组转化法求和

1

题型：单选题

|

单选题 · 5 分

3．已知等差数列的公差为，且，若，则m的值为（）

A12

B8

C6

D4

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的性质及应用

1

题型：简答题

|

简答题 · 12 分

32．已知两个无穷数列分别满足，，其中，设数列的前项和分别为，

（1）若数列都为递增数列，求数列的通项公式；

（2）若数列满足：存在唯一的正整数（），使得，称数列为“坠点数列”

①若数列为“5坠点数列”，求；

②若数列为“坠点数列”，数列为“坠点数列”，是否存在正整数，使得，若存在，求的最大值；若不存在，说明理由。

正确答案

an=2n-1; ；；的最大值为。

解析

（1）数列都为递增数列，∴，，

∴，

；

（2）①∵数列满足：存在唯一的正整数，使得，且，

∴数列必为，即前4项为首项为1，公差为2的等差数列，从第5项开始为首项5，公差为2的等差数列，

故；

② ∵，即，

而数列为“坠点数列”且，∴数列中有且只有两个负项．

假设存在正整数，使得，显然，且为奇数，而中各项均为奇数，∴必为偶数

i.当时，

当时，，故不存在，使得成立

ii.当时，

显然不存在，使得成立

iii．当时，

当时，才存在，使得成立

所以

当时，，构造：为，为

此时，，所以的最大值为。

考查方向

本题主要考查数列的综合运算

解题思路

1、求出an，bn;

2、利用定义求解，即可得到结果。

易错点

本题易在利用新定义求解时发生错误。

知识点

由递推关系式求数列的通项公式等差数列的基本运算等比数列的基本运算数列与不等式的综合

1

题型：简答题

|

简答题 · 12 分

17. 在等差数列中，，数列的前n项和.

（Ⅰ）求数列，的通项公式;

（Ⅱ）求数列的前n项和．

正确答案

见解析

解析

（Ⅰ）设等差数列的首项为，公差为d，则

数列的前n项和

当n=1时，，

当n2时，，对=4不成立，

所以，数列的通项公式为

（Ⅱ）n=1时，，

n2时，，

所以

n=1仍然适合上式，

综上，

考查方向

等比数列，等比数列的前n项和

解题思路

利用构造的等比数列求前n项和公式的求解

易错点

构造等比数列

知识点

由递推关系式求数列的通项公式等差数列的基本运算裂项相消法求和

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点