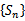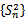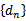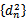- 等差数列
- 共618题
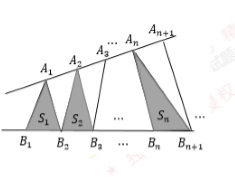
如图,点列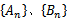
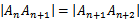
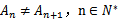
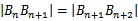
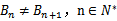
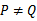
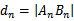
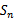
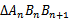
正确答案
知识点
8.已知





正确答案

解析
设公差为


解得


考查方向
解题思路
根据等差数列的通项以及求和列出方程组,求出基本量然后求特定项。
易错点
列方程求基本量致误
知识点
13.在等差数列{an}中,a4=-2,且al+a2+...+a10=65,则公差d的值是 。
正确答案
3
解析
先用性质解题:al+a2+...+a10=5(a4+ a7)=65,
所以(a4+ a7)= 13,
因此a7=11,
考查方向
解题思路
一是用基本量解题,列方程组;二是结合性质解题。
易错点
若用基本量表示前10项的和与a4,则运算要细心,否则就结合性质解题。
知识点
已知等差数列{an}的公差不为零,a1=25,且a1,a11,a13成等比数列.
18.求{an}的通项公式;
19.求a1+a4+a7+…+a3n-2.
正确答案
an=-2n+27,(2)Sn=(a1+a3n-2)=·(-6n+56)=-3n2+28n.
解析
解: (1)设{an}的公差为d.由题意,a=a1a13,[即(a1+10d)2=a1(a1+12d), 于是d(2a1+25d)=0.又a1=25,所以d=0(舍去),或d=-2.故an=-2n+27
考查方向
解题思路
本题考查等差数列和等比数列,数列的求和,解题步骤如下:设出等差数列的公差,由已知等比数列构造出一个方程解出符合题意的公差,写出数列的通项公式。
易错点
求和的时候将里面的项数弄错,等比中项性质。
正确答案
Sn=(a1+a3n-2)=·(-6n+56)=-3n2+28n.
解析
令Sn=a1+a4+a7+…+a3n-2.由(1)知a3n-2=-6n+31, 故{a3n-2}是首项为25,公差为-6的等差数列.
从而Sn=(a1+a3n-2)=·(-6n+56)=-3n2+28n.
考查方向
解题思路
要求的数列也是一个等差数列,利用等差数列的前n项和公式解答即可。
易错点
求和的时候将里面的项数弄错,等比中项性质。
4.等差数列

正确答案
解析
由题可知

∴

考查方向
本题主要考查等差数列的相关知识与性质,意在考查考生的运算求解能力及等差数列通项和求和公式的应用能力,在近几年的各省高考题出现的频率较高,较易。
解题思路
1、先根据


2、再要根据等差数列求和公式
易错点
本题易出现的问题是选择那个求和公式完成而造成计算繁琐。
知识点
5.设等差数列



正确答案
解析
由


考查方向
解题思路
结合等差数列的性质先求出第7项,然后
易错点
等差数列前奇数项的和不会用中间项表示。
知识点
6.设




正确答案
解析
根据所给的已知条件,因为

考查方向
解题思路
根据题意和等差数列的性质求解
易错点
不能准确的利用等差数列的性质
知识点
14.我们知道,把所有的正整数按照不同的方式排列,就会出现很多不同的意义。现在把所有正整数按从小到大的顺序排成如图所示的数表,其中第






正确答案
1004
解析
最后一个数是首项为1,等比为2的前n项和,n+1表示行数,当n=10时,即第11行的最后一个数为2047,第11行共有
考查方向
解题思路
最后一个数是首项为1,等比为2的前n项和,n+1表示行数,当n=10时,即第11行的最后一个数为2047,第11行共有
易错点
找不到规律;推理出错,计算错误都是导致出错的原因。
知识点
16.已知等差数列





(1)
(2)
(3)
(4)当

(5)
其中正确的有 (把你认为正确的说法都写上)
正确答案
(1)(2)(4)
解析
由
















考查方向
本题主要考查了函数与数列的联系及等差数列的公式与性质。
易错点
不知道如何处理这个式子
知识点
5.等差数列




正确答案
解析
由


考查方向
考查等差数列前n项和公式
解题思路
根据前n项和公式求公差
易错点
项数和项弄混淆
知识点
扫码查看完整答案与解析