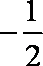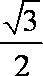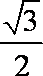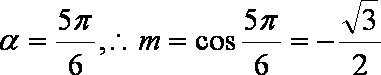- 等差数列
- 共618题
已知数列{


(1)求

(2)证明:不等式

正确答案
见解析
解析
(1)解:由题意,得
(2)证明:①当

②设当

则当

而
所以
即当
由①②,得不等式

知识点
已知数列








(1)若

(2)是否存在正整数k,使

正确答案
(1)1(2)不存在
解析
解析:(1)由题意知,

∴


∴





∴


(2)记




① 若



② 若



③ 若



因为

综上:不存在
知识点
已知数列


(1)当



(2)试求出数列





正确答案
见解析
解析
解析:(1)当



当











综上讨论,满足条件的数列有三个:
1,2,3或1,2,-2或1,-1,1.············································································· 6分
知识点
在数列





(1)当



并给出证明;
(2)求出所有的正整数

正确答案
见解析。
解析
(1)由已知得

所以



猜想:

下面用数学归纳法证明:
①当
②假设当

将

则当

故当
根据①,②可得,

(2)将


则

设

即
又


故
所以
由



所以当
知识点
已知函数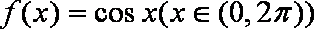
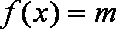
正确答案
解析
设两个根依次为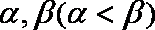
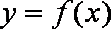
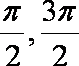
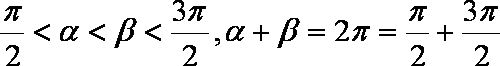
知识点
某工厂生产一种产品的成本费共由三部分组成:①原材料费每件50元;②职工工资支出


(1)把每件产品的成本费

(2)如果该厂生产的这种产品的数量


正确答案
见解析
解析
(1)

由基本不等式得:
当且仅当

所以

(2)设总利润

所以
= 
当



所以
所以当


所以生产100件产品时,总利润最高,且最高利润为
知识点
已知数列





(1)求

(2)求证:对一切正整数

正确答案
见解析。
解析
(1)由

由

(2)


猜想:
证明:①当
②假设当

那么,当



又由

所以
所以
所以
即当
综上可得,对一切正整数

知识点
设数列




(1)求数列
(2)若

正确答案
见解析
解析
(1)因为点


当

两式相减得

又当

所以数列



(2)由(1)知,
记数列



两式相减得
所以数列

知识点
若sin2x、sinx分别是sinθ与cosθ的等差中项和等比中项,则cos2x的值为
正确答案
解析
依题意有

由①2-②×2得,

又由


知识点
设等差数列






(1)求数列

(2)设



正确答案
见解析
解析
(1)由题意,




数列

(2)
当

当
(法一)
(法二)

知识点
扫码查看完整答案与解析