导数的加法与减法法则
共661题

· 导数的加法与减法法则

导数的加法与减法法则
共661题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

若变量x，y满足约束条件则z=2x+y的最大值为（　　）

正确答案

解析

作出可行域，作出目标函数线，

可得直线与y=x与3x+2y=5的交点为最优解点，

∴即为B（1，1），当x=1，y=1时zmax=3。

故选C。

知识点

导数的加法与减法法则

题型：填空题

填空题 · 5 分

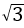
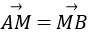
已知抛物线C：y2=2px（p＞0）的准线l，过M（1，0）且斜率为的直线与l相交于A，与C的一个交点为B，若，则p=　_________

正确答案

解析

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

设,则满足的数组共有( )

A1组

B2组

C3组

D无数组

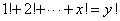
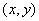
正确答案

解析

略

知识点

导数的加法与减法法则

题型：简答题

简答题 · 12 分

已知函数，且恒成立。

（1）求t的值；

（2）求为何值时，上取最大值；

（3）设若单调递增，求的取值范围。

正确答案

见解析。

解析

（1）由题意可知，的定义域为，且是的最小值，又

所以当时，；当时，.从而在上是减函数，在上是增函数，故

显然在的定义域恒成立，所以

下面分情况讨论当的取值情况。

当显然不可能成立；

当

且

及上恒成立。

故所求的取值范围为

知识点

导数的加法与减法法则

题型：简答题

简答题 · 12 分

已知集合中的元素都是正整数，且，对任意的且，有。

（1）求证：；

（2）求证：；

（3）对于，试给出一个满足条件的集合。

正确答案

见解析。

解析

（1）证明：依题意有，又，

因此。

可得。

所以。

即。

（2）证明：由（1）可得。

又，可得，因此。

同理，可知。

又，可得，

所以均成立。

当时，取，则，

可知。

又当时，。

所以。

（3）解：对于任意，，

由可知，

，即。

因此，只需对，成立即可。

因为；；；，

因此可设；；；；。

由，可得，取。

所以满足条件的一个集合。

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

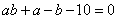
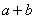
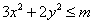
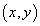
设a，b为大于1的正数，并且，如果的最小值为m，则满足的整点的个数为（）

D11

正确答案

解析

略

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

双曲线的左右焦点分别为，且恰为抛物线的焦点，设双曲线与该抛物线的一个交点为，若是以为底边的等腰三角形，则双曲线的离心率为（）

正确答案

解析

略

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

已知x、y使方程x2+y2-2x -4y + 4 = 0，则的最小值是（）

正确答案

解析

略

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

若是等差数列，，则使前项和成立的最大正数是（）

A48

B47

C46

D45

正确答案

解析

略

知识点

导数的加法与减法法则

题型：填空题

填空题 · 5 分

某商场销售甲、乙、丙三种不同型号的钢笔，甲、乙、丙三种型号钢笔数量之比依次为 2：3：4.现用分层抽样的方法抽出一个容量为n的样本，其中甲型钢笔有12支，则此样本容量n=　　。

正确答案

解析

由n•=12，求得 n=54，

故答案为 54。

知识点

导数的加法与减法法则

继续学习学习下一知识点

下一知识点 : 导数的乘法与除法法则

百度题库 > 高考 > 理科数学 > 导数的加法与减法法则

扫码查看完整答案与解析