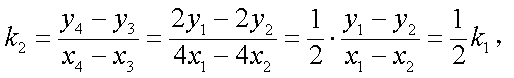- 导数的加法与减法法则
- 共661题
某几何体的三视图如图示,则此几何体的体积是
正确答案
解析
此几何体为半个圆锥与半个圆柱的组合体,体积
知识点
设曲线C:
(1)求函数f(x)的极值;
(2)数列{an}满足
(3)对于曲线C上的不同两点A(x1,y1),B (x2,y2),x1<x2,求证:存在唯一的
正确答案
见解析
解析
(1)
当


∴当


(2)∵


…………(7分)
假设数列


因此,数列
(3)(方法1)∵

即




∵





∵

∴函数


又∵


∴函数


(方法2)∵

即


设

再设

∴

∴
∴方程

∵一次函数在
∴方程

知识点
在平面直角坐标系xOy中,已知抛物线C: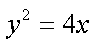
为抛物线C上异于顶点的动点,直线MF交抛物线C于另一点N,链接ME,NE并延长分别交
抛物线C与点P,Q。
(1)当MN 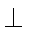
(2)当直线MN,PQ的斜率存在且分别记为k1,k2时,求证: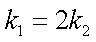
正确答案
见解析。
解析
(1)抛物线C: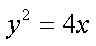
当MN 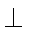
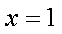
将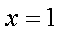
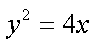
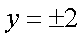
不妨设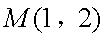
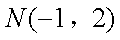
则直线ME的方程为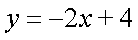
由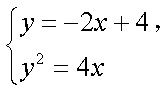
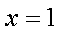
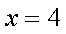
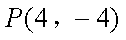
同理得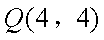
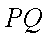
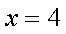
故直线PQ与x轴的交点坐标(4,0),
(2)设直线MN的方程为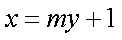
并设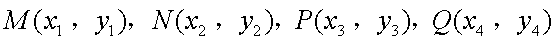
由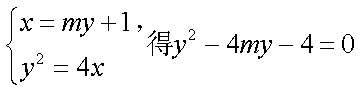
于是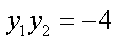
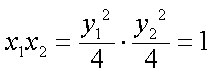
设直线MP的方程为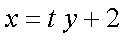
由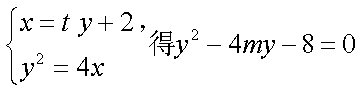
所以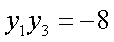
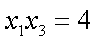
同理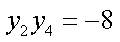
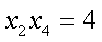
由①②③④⑤⑥,得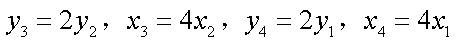
即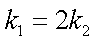
知识点
设






(1)证明:当


(2)记

正确答案
见解析。
解析
(1)当


∵


∴
=
∴当

同理可证,当

(2)由
=
=
=
又由



知识点
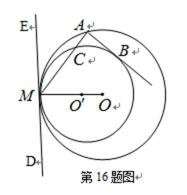
如图,过半径为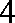
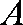
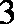
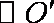
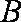
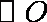

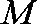
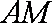
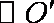

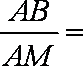
正确答案
解析
作两圆的公切线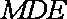
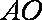
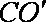
所以
由弦切角定理知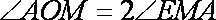
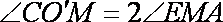
则
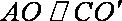
所以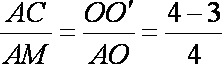

知识点
扫码查看完整答案与解析