导数的加法与减法法则
共661题

· 导数的加法与减法法则

导数的加法与减法法则
共661题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

已知向量。

（1）当时，求的值；

（2）设函数，已知在△ ABC中，内角A、B、C的对边分别为，若 ,求（）的取值范围。

正确答案

见解析

解析

（1）

（2）+

由正弦定理得或

因为，所以

所以

知识点

导数的加法与减法法则

题型：填空题

填空题 · 5 分

在△ABC中，若9cos2A﹣4cos2B=5，则的值为　　。

正确答案

解析

在△ABC中，∵9cos2A﹣4cos2B=5，∴9（1﹣2sin2A ）﹣4（1﹣2sin2B）=5，

化简可得 9sin2A=4sin2B，故有 =。

由正弦定理可得 ==，

故答案为，

知识点

导数的加法与减法法则

题型：简答题

简答题 · 14 分

如图，在四棱锥P‐ABCD中，四边形ABCD为正方形，PA⊥平面ABCD，E为PD

的中点，求证：

（1）PB∥平面AEC；

（2）平面PCD⊥平面PAD。

正确答案

见解析

解析

（1）证明：连结交于点，连结。

因为为中点，为中点，

所以，

因为平面，平面，

所以平面，

（2）证明：因为平面，平面，所以，

因为在正方形中且，

所以平面。

又因为平面，所以平面平面。

知识点

导数的加法与减法法则

题型：简答题

简答题 · 12 分

由于雾霾日趋严重，政府号召市民乘公交出行.但公交车的数量太多会造成资源的浪费，太少又难以满足乘客需求.为此，某市公交公司在某站台的名候车乘客中进行随机抽样，共抽取10人进行调查反馈，所选乘客情况如下表所示：

（1）估计这名乘客中候车时间少于分钟的人数；

（2）现从这10人中随机取3人，求至少有一人来自第二组的概率；

（3）现从这10人中随机抽取3人进行问卷调查，设这3个人共来自个组，求的分布列及数学期望.

正确答案

见解析

解析

（1）候车时间少于分钟的人数为人； ………3分

（2）设“至少有一人来自第二组为事件A”

…………6分

（3）的可能值为1，2，3

…………9分

所以的分布列为

…………10分

…………12分

知识点

导数的加法与减法法则

题型：简答题

简答题 · 14 分

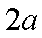
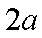
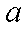
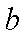
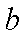
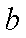
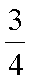
随着机构改革开作的深入进行，各单位要减员增效，有一家公司现有职员人（140＜＜420，且为偶数，每人每年可创利万元. 据评估，在经营条件不变的前提下，每裁员1人，则留岗职员每人每年多创利0.01万元，但公司需付下岗职员每人每年0.4万元的生活费，并且该公司正常运转所需人数不得小于现有职员的，为获得最大的经济效益，该公司应裁员多少人？

正确答案

见解析

解析

设裁员x人，可获得的经济效益为y万元，则

依题意

（1）当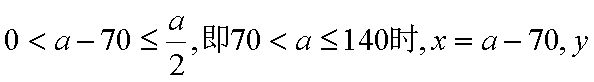取到最大值；

（2）当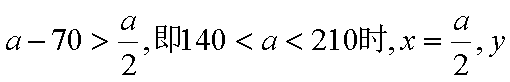取到最大值；

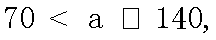
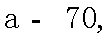
答：当公司应裁员为经济效益取到最大值

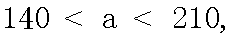
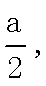
当公司应裁员为经济效益取到最大值

知识点

导数的加法与减法法则

继续学习学习下一知识点

下一知识点 : 导数的乘法与除法法则

百度题库 > 高考 > 理科数学 > 导数的加法与减法法则

扫码查看完整答案与解析