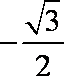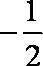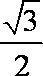- 导数的加法与减法法则
- 共661题
我校开办复读班有几十年的历史,据历年经验理科生当年上二本以上的学生复读一年上一本的概率为



(1)假若2014年高考与2013年高考难度及分数线不变的前提下,判断历年的经验是否正确,说明理由.
(2)综合各种情况分析,可以假设高考分数高于



正确答案
见解析
解析
(1)不合理,二本、三本给出的是一个分数段,与分数在该段的分布位置有关;以二本最低分计算上一类的概率为

(2)
知识点
已知
(1)求

(2)设λ1,λ2>0,且λ1+λ2=1,x1>0,x2>0,证明:

(3)证明:若

正确答案
见解析
解析
(1)F(x)=-lnx-
当x∈(0,1)时F′(x)>0,x∈(1,+∞)时F′(x)<0
∴F(x)在(0,1)递增,在(1,+∞)递减,
F(x)max=F(0)=0;∴当





(2)证明:设λ1>0,λ2>0且λ1+λ2=1
令x3=λ1 x1+λ2 x2,则
x1-x3=λ2(x1-x2) x2-x3=λ1(x2-x1)
由(1)知f (x1) -f (x3) ≥f′(x3)( x1-x3) =λ2 f′(x3)( x1-x2) ………①
f (x2) -f (x3) ≥f′(x3)( x2-x3) =λ1 f′(x3)( x2-x1) ………②
①×λ1+②×λ2,得
λ1 f (x1) +λ2 f (x2) -(λ1+λ2)f (x3) ≥λ1λ2 f′(x3) ( x1-x2)+λ1λ2 f′(x3)( x2-x1)=0
∴λ1 f (x1) +λ2 f (x2) ≥(λ1+λ2)f (x3) =f (x3) =f(λ1 x1+λ2 x2)…………8分
猜想:λi>0,xi>0(i=1,2,…n)且λ1+λ2+
λ1 f (x1) +λ2 f (x2) +…+λn f (xn) ≥f(λ1 x1+λ2 x2+…+λn xn)…………9分
(3)证明:令λi=
则有λ1+λ2+…+λn=1
由猜想结论得:


≥-ln(


=-ln
∴a1lna1+a2lna2+…+anlnan≥(a1+a2+…+an) ln
即

法2:令

即


a1lna1+a2lna2+…+anlnan≥

知识点
已知数列


(1)求

(2)设

正确答案
(1)

解析
解析:(1)由已知


又


(2)当

即
故有




∴
∴
知识点
将曲线C1:

正确答案
见解析。
解析


知识点
已知二次函数g(x)对任意实数x都满足


(1)求 g(x)的表达式;
(2)设



正确答案
见解析
解析
解析: (1)设
所以



(2)因为对



于是

记
所以函数

所以
知识点
已知A、B两点分别在两条互相垂直的直线



正确答案
解析
由已知两直线互相垂直得



知识点
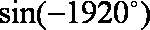
正确答案
解析
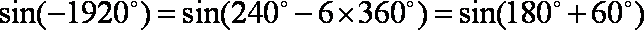
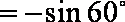
知识点
已知方程


正确答案
解析








知识点
已知








正确答案
解析

知识点
定义在R上的函数



(1)求

(2)
(3)设

正确答案
见解析
解析
(1)


由①②联立解得: 



由


(2)设

依题意知:当









(3)设

设
当





当





当




当




综上所述:
当

当

当

当

知识点
扫码查看完整答案与解析