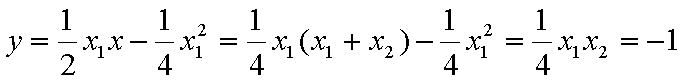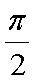- 导数的加法与减法法则
- 共661题
在四棱锥




(1)当

(2)若



正确答案
见解析
解析
(1)当

又因为


又



为


则
设
要使
所以

由此可知

当且仅当



由此可知

则


取平面
则

因此二面角
知识点
设




①若



②若


③ 若



④ 若



其中错误命题的序号是
正确答案
解析
根据线面垂直的性质和判断可知,②③正确,错误的为①④,选B.
知识点
已知函数

(1)求函数
(2)若函数




正确答案
(1)
(2)
解析
(1)



当

函数


(






即


知识点
已知



正确答案
解析
本题为几何概率.区域



知识点
已知椭圆
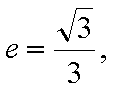
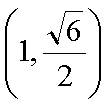
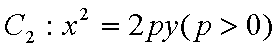
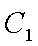
(1)过F的直线与抛物线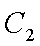
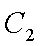
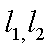
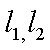
(2)从圆O: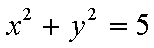
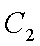
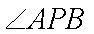
正确答案
见解析
解析
(1)由于椭圆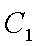
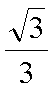
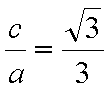
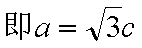
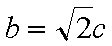
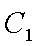
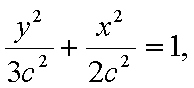
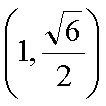
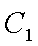
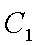
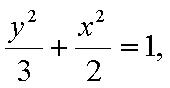
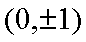
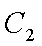
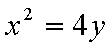
易知直线MN的斜率一定存在,设为k,则直线MN的方程为y=kx+1,代入抛物线的方程得到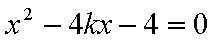
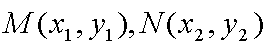
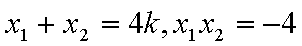
由于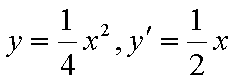
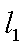
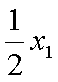
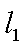
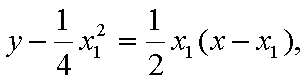
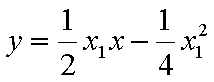
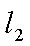
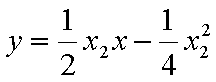

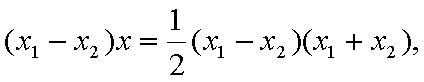
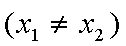

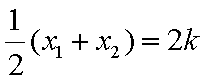
,即点Q(2k,-1),故点Q的轨迹方程是y=-1
(2)当这两条切线中有一条切线的斜率不存在时,根据对称性,不妨设点P在第一象限,则此时点P的横坐标为

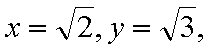
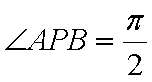
当这两条切线的斜率都存在时,设点P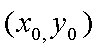

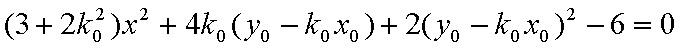
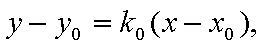
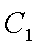
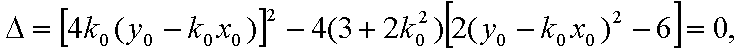
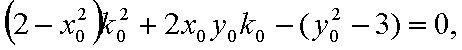
设切线PA,PB的斜率分别为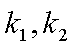
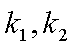
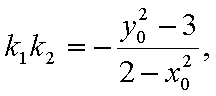
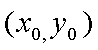
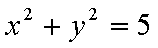
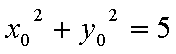
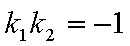
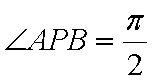
综上可知,角APB的大小为定值,且这个定值为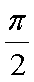
知识点
某几何体的三视图如图所示,且该几何体的体积是
正确答案
解析
由三视图可知,这个几何体是一个底面为直角梯形的四棱锥,底面积为S=


知识点
为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚,为了更好地了解市民的态度,在普通行人中随机选取了200人进行调查,得到如下数据:
(1)若用表中数据所得频率代替概率,则
的概率的差是多少?
(2)若从这5种处罚金额中随机抽取2种不同的金额进行处罚,在两个路口进行试验。
①求这两种金额之和不低于20元的概率;
②若用X表示这两种金额之和,求X的分布列和数学期望。
正确答案
见解析
解析
解:(1)由条件可知,处罚10元会闯红灯的概率与处罚20元会闯红灯的概率的差是:
(2)①设“两种金额之和不低于20元”的事件为

故所求概率为
②根据条件,

知识点
如图,四棱锥








(1)当



(2)在(1)的条件下,求二面角
正确答案
(1)
解析
(1)在梯形



∴


∴
连接






在

即


(2)方法一:在等腰直角











在平面












在





由




代入解得:
在



∴二面角

方法二:以



设






设






设



又


∴
∴二面角

知识点
函数
(1)求函数
(2)求函数


正确答案
见解析
解析
解(1)由图知
∴


∵


∴

∵


(2)由
解得函数
函数

知识点
将10个白小球中的3个染成红色,3个染成黄色,试解决下列问题:
(1)求取出3个小球中红球个数
(2)求取出3个小球中红球个数多于白球个数的概率。
正确答案
见解析
解析
(1)因为从10个球中任取3个,其中恰有
所以随机变量

(2)设“取出的3个球中红球数多于白球数”为事件



又
故
知识点
扫码查看完整答案与解析