- 导数的加法与减法法则
- 共661题
在四棱锥




(1)当

(2)若



正确答案
见解析
解析
(1)当

又因为


又



为


则
设
要使
所以

由此可知

当且仅当



由此可知

则


取平面
则

因此二面角
知识点
设




①若



②若


③ 若



④ 若



其中错误命题的序号是
正确答案
解析
根据线面垂直的性质和判断可知,②③正确,错误的为①④,选B.
知识点
已知



正确答案
解析
本题为几何概率.区域



知识点
已知椭圆
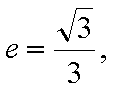
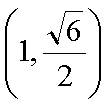
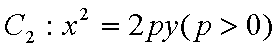
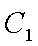
(1)过F的直线与抛物线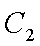
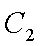
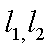
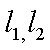
(2)从圆O: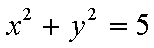
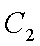
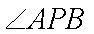
正确答案
见解析
解析
(1)由于椭圆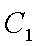
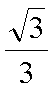
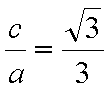
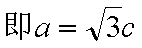
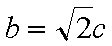
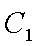
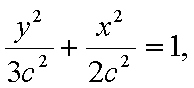
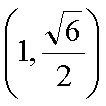
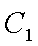
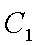
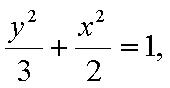
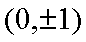
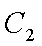
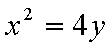
易知直线MN的斜率一定存在,设为k,则直线MN的方程为y=kx+1,代入抛物线的方程得到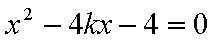
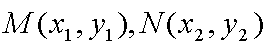
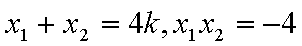
由于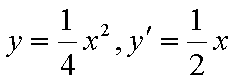
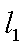
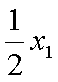
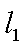
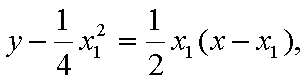
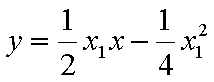
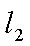
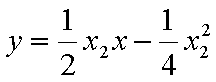

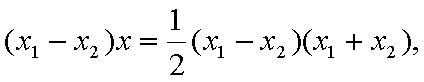
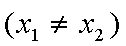

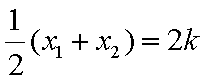
,即点Q(2k,-1),故点Q的轨迹方程是y=-1
(2)当这两条切线中有一条切线的斜率不存在时,根据对称性,不妨设点P在第一象限,则此时点P的横坐标为

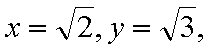
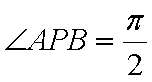
当这两条切线的斜率都存在时,设点P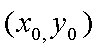

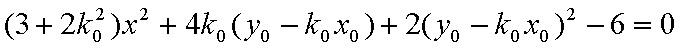
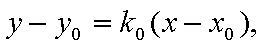
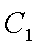
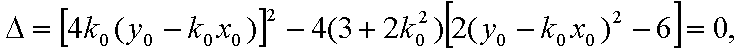
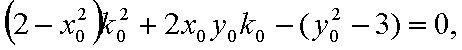
设切线PA,PB的斜率分别为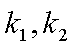
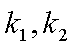
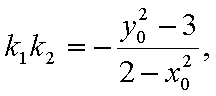
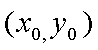
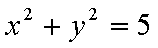
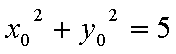
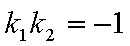
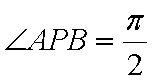
综上可知,角APB的大小为定值,且这个定值为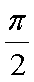
知识点
某几何体的三视图如图所示,且该几何体的体积是
正确答案
解析
由三视图可知,这个几何体是一个底面为直角梯形的四棱锥,底面积为S=


知识点
扫码查看完整答案与解析