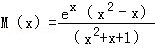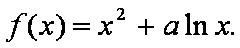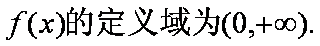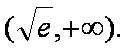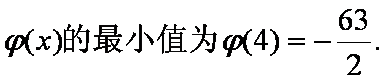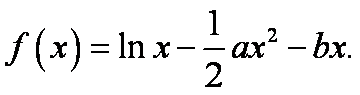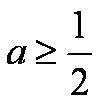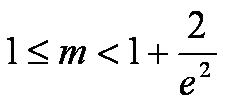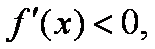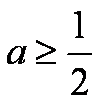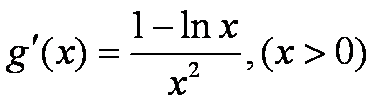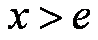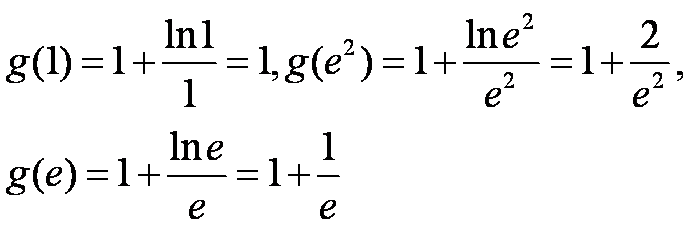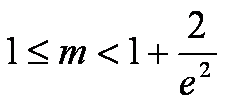- 导数的加法与减法法则
- 共661题
盒中装有形状,大小完全相同的5个球,其中红色球3个,黄色球2个,若从中随机取出2个球,已知其中一个为红色,则另一个为黄色的概率为
正确答案
解析
记红色球分别为a、b、c,黄色球分别为d、e,因为随机取出2个球,其中一个为红色,所以所有的基本事件为(a,b),(a,c),(b,c),(a,d),(a,e),(b,d),(b,e),(c,d),(c,e)共9个,符合题意的基本事件为:(a,d),(a,e),(b,d),(b,e),(c,d),(c,e)共6个,因此,另一个为黄色的概率为:P=
知识点
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系。已知曲线C1的极坐标方程为

(1)写出曲线C1与直线l的直角坐标方程;
(2)设Q为曲线C1上一动点,求Q点到直线l距离的最小值。
正确答案
见解析
解析
解析:
(1)

(2)设



当且仅当


知识点
如果双曲线的离心率
①双曲线

③在双曲线

④在双曲线

其中正确命题的序号为( )
正确答案
解析
略
知识点
计划将排球、篮球、乒乓球


正确答案
解析
若



知识点
设函数
(1)判断函数f(x)在(0,+∞)上的单调性;
(2)证明:对任意正数a,存在正数x,使不等式f(x)-1<a成立。
请考生在22、23、24中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做第一个题目计分,作答时请用2B铅笔在答题卡上将所选题号后的方框涂黑。
正确答案
见解析
解析
(1) 由题意知:
令h(x)=(x-1)ex+1,则h‘(x)=x ex>0,
∴h(x)在(0,+∞)上是增函数,
又h(0)=0,∴h(x)>0,则f’(x)>0,
∴f(x)在(0,+∞)上是单调增函数.
(2) 
令G(x)= ex-(a+1)x-1, G’(x)=ex-(a+1),
由G‘(x)=0得:x=ln(a+1),
当0<x< (ln(a+1)时,G’(x)<0,
当x>ln(a+1)时,G‘(x)>0,
∴当x=ln(a+1)时,G(x)min=a-(a+1)ln(a+1),
令

又
∴当a>0时,

即当x=ln(a+1)时,G(x)min=a-(a+1)ln(a+1)<0.
故存在正数x=ln(a+1),使不等式F(x)-1<a成立,
知识点
把函数


正确答案
解析
解:


再将图象向右平移


故选A。
知识点
已知函数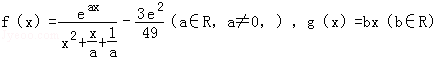
(1)当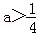
(2)当a=1时,若在区间[2,+∞)上存在一点x0,使得f(x0)<g(x0)成立,求b的取值范围。
正确答案
见解析
解析
(1)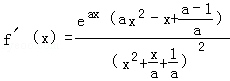
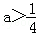
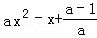
所以 ①当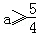
②当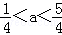
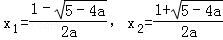
当x变化时,由f'(x)和f(x)的变化可知:
f(x)在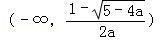
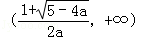
f(x)在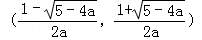
(2)考查反面情况:∀x∈[2,+∞),f(x)≥g(x)恒成立,
即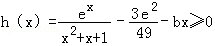
首先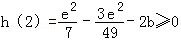
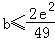
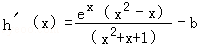
因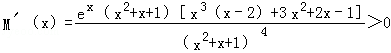
所以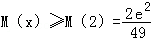
所以当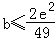
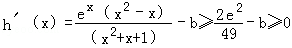
又h(2)≥0,所以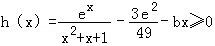
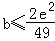
综上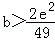
知识点
实数x,y满足
正确答案
解析
由





平移至经过



最大值,代入



知识点
已知函数
(1)当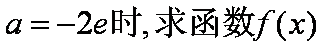
(2)若函数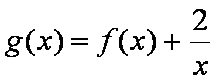
正确答案
见解析
解析
解析:
(1)函数
当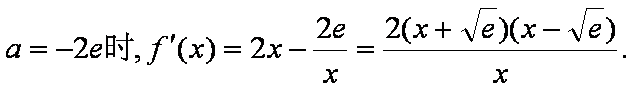
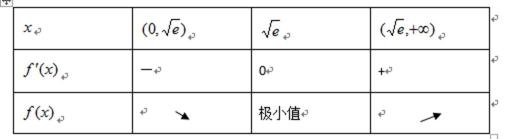
当x变化时,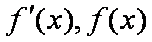
由上表可知,函数
单调递增区间是
极小值是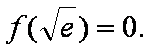
(2)由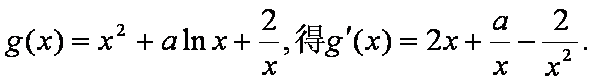
又函数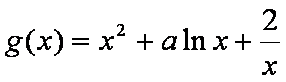
则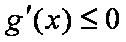
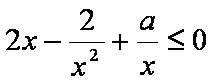
即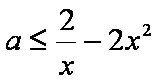
又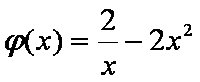
所以
所以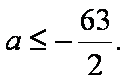
知识点
设函数
(1)当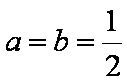
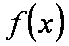
(2)令
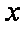

(3)当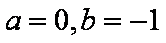
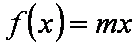
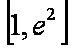
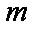
正确答案
(1)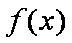
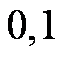

(2)
(3)
解析
(1)解:依题意,知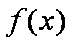
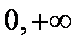
当 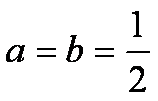
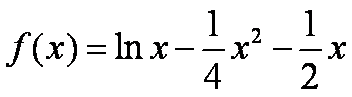
令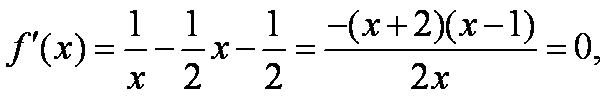
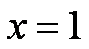
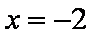
当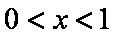
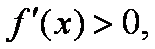
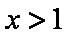
所以f(x)的单调增区间是(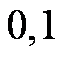

(2)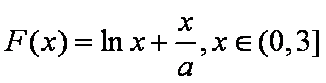
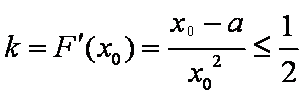
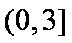
所以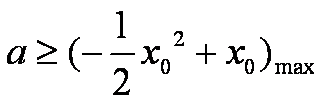
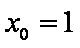
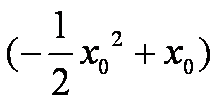
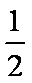
所以
(3)当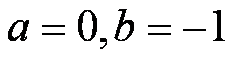
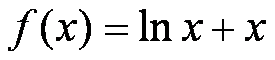
由
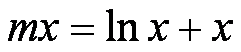
又因为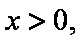
要是方程
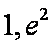

令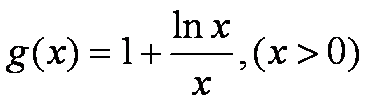
由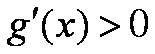
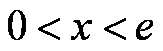
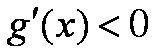
所以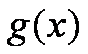

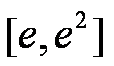
所以
所以
知识点
扫码查看完整答案与解析