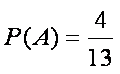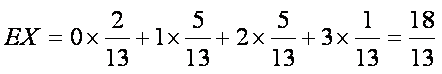- 导数的加法与减法法则
- 共661题
已知椭圆







(1)当
(2)直线

正确答案
见解析
解析
解析:(1)由题意

于是圆心坐标为



即




所以



(2)假设相切, 则



故直线

知识点
已知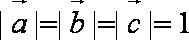
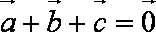
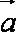
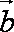
正确答案
解析
法1: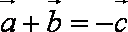
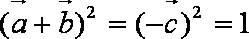
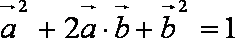
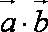
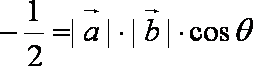
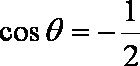
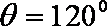
法2:由模都为1及向量的加法法则知,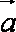
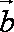
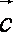
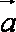
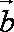
知识点
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,其数值越大说明空气污染状况越严重,对人体健康的危害也就越大。根据国家标准,指数在0-50之间时,空气质量为优;在51-100之间时,空气质量为良;在101-150之间时,空气质量为轻度污染;在151-200之间时,空气质量为中度污染;在大于200时,空气质量为重度污染。环保部门对某市5月1日至5月15日空气质量指数预报如下表:
某人选择5月1日至5月13日某一天到达该市,并停留三天.
(1)求此人到达当日空气重度污染的概率;
(2)设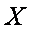
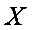
(3)根据上表判断从哪天开始连续三天的空气质量指数方差最大(不要求计算,只写出结果).
命题意图: 考查概率统计的基本运算及随机变量分布列,中档题。
正确答案
见解析。
解析
(1)记事件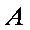
(2)此人在该市停留期间空气质量优良天数统计如下表:
所以随机变量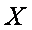
所以
(3)从5月3日开始连续三天的空气质量指数方差最大.
知识点
户外运动已经成为一种时尚运动,某单位为了了解员工喜欢户外运动是否与性别有关,对本单位的50名员工进行了问卷调查,得到了如下列联表:
已知在这50人中随机抽取1人抽到喜欢户外运动的员工的概率是
(1)请将上面的列联表补充完整;
(2)是否有99.5﹪的把握认为喜欢户外运动与性别有关?并说明你的理由;
(3)经进一步调查发现,在喜欢户外运动的10名女性员工中,有4人还喜欢瑜
伽.若从喜欢户外运动的10位女性员工中任选3人,记
的人数,求
下面的临界值表仅供参考:
(
正确答案
见解析。
解析
(1)



(2)


(3)




知识点
某中学篮球队进行投篮训练,每人在一轮练习中最多可投篮4次,且规定一旦投进即停止该轮练习,否则一直投到4次为止,已知队员甲每次投进的概率为
(1)求一轮练习中,队员甲的投篮次数


(2)在一轮练习中,队员甲至少投篮3次的概率。
正确答案
见解析
解析
解析:
(1)分布列为
期望为 
(2)
(2)向量法:
设



知识点
如图一个空间几何体的正视图、左视图、俯视图均为全等的等腰直角三角形,如果直角三角形的直角边长都为1,那么这个几何体的体积为 ( )
正确答案
解析
三视图所对应的空间几何体是一个三棱锥,其底面是边长为1的等腰直角三角形,三棱锥的高是1,故其体积是
知识点
已知函数
(1)若函数

(2)设直线







正确答案
见解析
解析
(1)

令



若
若


若
综上 若


若
(2)
设






设

当




且


知识点
已知数列





(1)求数列
(2)记



正确答案
见解析
解析
(1)由已知得
所以
(2)
当


当

①-②得
所以


(3)由(2)知,


所以当


所以

知识点
函数



正确答案
解析
利用换元法,将


当



可知当



故



知识点
各项都是正数的等比数列



正确答案
解析
由题意







知识点
扫码查看完整答案与解析