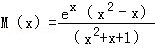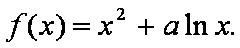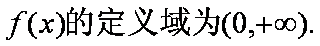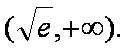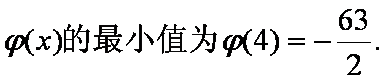- 导数的加法与减法法则
- 共661题
如果双曲线的离心率
①双曲线

③在双曲线

④在双曲线

其中正确命题的序号为( )
正确答案
解析
略
知识点
计划将排球、篮球、乒乓球


正确答案
解析
若



知识点
已知函数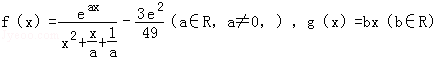
(1)当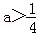
(2)当a=1时,若在区间[2,+∞)上存在一点x0,使得f(x0)<g(x0)成立,求b的取值范围。
正确答案
见解析
解析
(1)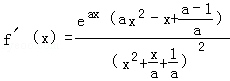
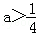
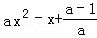
所以 ①当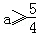
②当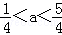
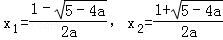
当x变化时,由f'(x)和f(x)的变化可知:
f(x)在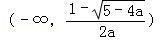
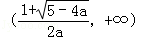
f(x)在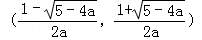
(2)考查反面情况:∀x∈[2,+∞),f(x)≥g(x)恒成立,
即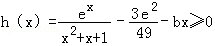
首先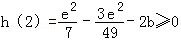
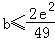
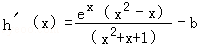
因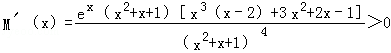
所以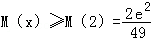
所以当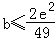
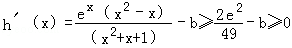
又h(2)≥0,所以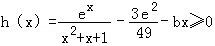
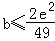
综上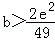
知识点
实数x,y满足
正确答案
解析
由





平移至经过



最大值,代入



知识点
已知函数
(1)当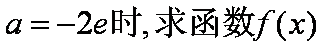
(2)若函数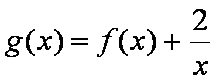
正确答案
见解析
解析
解析:
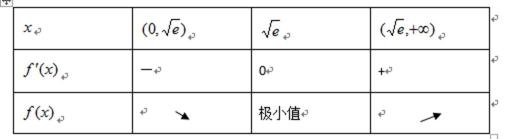
(1)函数
当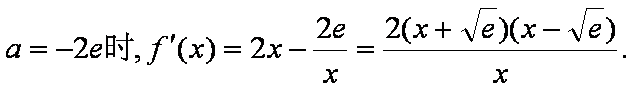
当x变化时,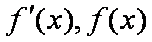
由上表可知,函数
单调递增区间是
极小值是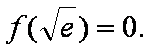
(2)由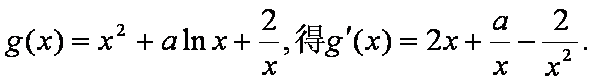
又函数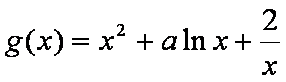
则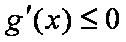
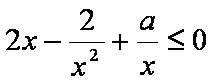
即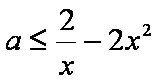
又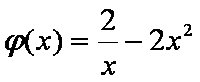
所以
所以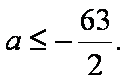
知识点
扫码查看完整答案与解析