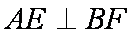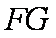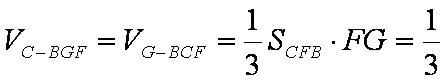- 导数的加法与减法法则
- 共661题
函数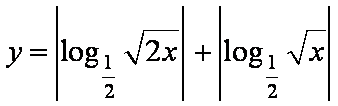
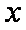
正确答案
解析
略
知识点
已知函数





正确答案
解析
作函数











知识点
直线



正确答案
解析
由








解得n=2
又直线y=5截曲线的弦长与直线y=-1截曲线的弦长相等且不为0,则可得m>3. 故选D
知识点
已知函数f(x)=ex﹣ae﹣x,若f′(x)≥2
正确答案
[3,+∞)
解析
函数的导数f'(x)=ex+ae﹣x,所以由f′(x)≥2


设t=ex,则t>0,则函数

即实数a的取值范围是[3,+∞)。
知识点
已知函数
(1)求函数
(2)若


正确答案
见解析
解析
(1)

由


∴函数


(2)∵


∵


∴
知识点
已知函数
(1)若函数


(2)在(1)的条件下,对任意



(3)若





正确答案
见解析
解析
(1)
(2)由(1)知,
故
(3)
则
①若


②若






知识点
已知函数



正确答案
5
解析
略
知识点
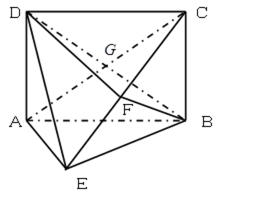
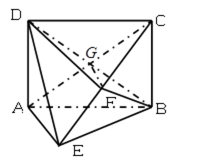
如图,在三棱锥





(1)求证:
(2)设点



正确答案
见解析
解析
证明:(1)方法一:由


又


故
同理可得


则

方法二:由已知可得












(2)方法一:由(1)的证明过程知







由已知可得



又

故


方法二: 由(I)的证明过程知
标系,则
可得

的一个法向量为




则


知识点
如图所示,矩形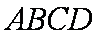
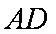
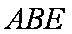
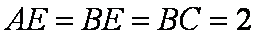
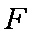
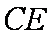
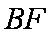
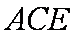
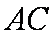
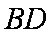

(1)求证: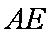
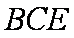
(2)求证: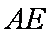
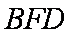
(3)求三棱锥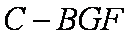
正确答案
见解析。
解析
(1)证明:∵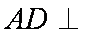
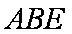
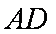
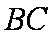
∴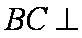
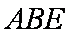

又

∴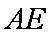
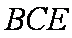
(2)由题意可得
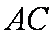
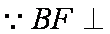
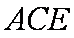

而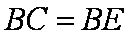
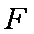
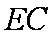
在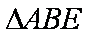
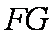
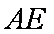
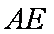
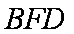
(3)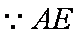
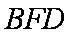
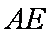
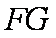
而∴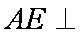
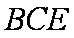
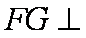
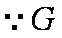
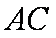

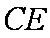
∴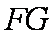
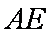
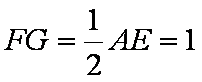
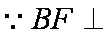
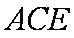

∴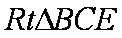
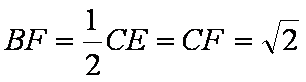
∴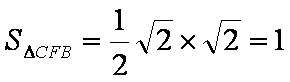
∴
知识点
如图,在△




















(1)求证:

(2)设



正确答案
见解析
解析
(1)因为




因为平面




同理,




所以平面



(2)以C为原点,





则






平面

平面

由
化简得

知识点
扫码查看完整答案与解析