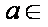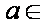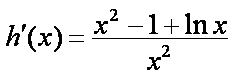- 导数的加法与减法法则
- 共661题
如图,在直角三角形




(1)若

(2)试判断
(3)求

正确答案
见解析
解析
(1)[解法1] 


,即




[解法2]将已知方程两边平方,得

即



(2)[解法1]以O为原点,建立平面直角坐标系,设



则由

[解法2]
所以,
(3) [解法1]作




[解法2] 



知识点
已知函数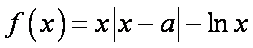
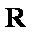
(1)若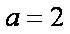
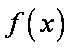
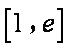
(2)若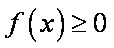
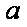
注: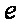
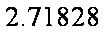
正确答案
见解析
解析
解:(1) 若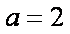
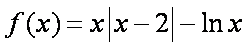
当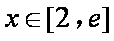
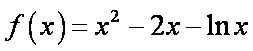

所以函数
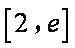
当
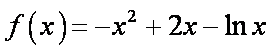
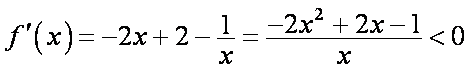
所以函数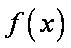
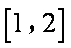
所以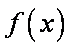
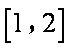
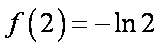
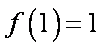
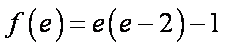
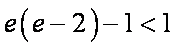
所以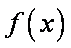
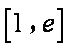
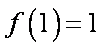
(2) 函数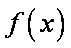
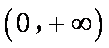
由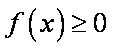
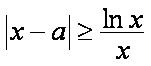
(ⅰ)当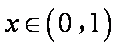
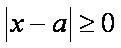
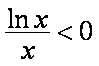
不等式(*)恒成立,所以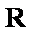
(ⅱ)当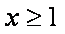
①当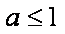
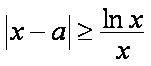
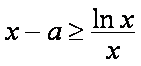
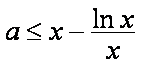
现令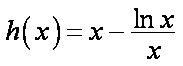
因为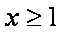
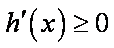
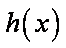
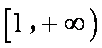
从而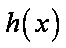
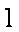
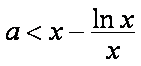
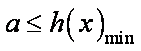
所以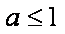
②当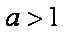
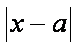
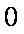
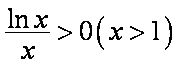
综上可得,满足条件的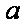
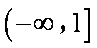
知识点
已知直角坐标系xOy中,直线l的参数方程为

正确答案
解析
直线l普通方程为



知识点
已知A、B为抛物线C:y2 = 4x上的两个动点,点A在第一象限,点B在第四象限l1、l2分别过点A、B且与抛物线C相切,P为l1、l2的交点。
(1)若直线AB过抛物线C的焦点F,求证:动点P在一条定直线上,并求此直线方程;
(2)设C、D为直线l1、l2与直线x = 4的交点,求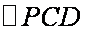
正确答案
(1)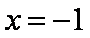
(2)
解析
(1)设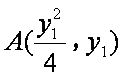
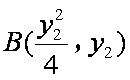
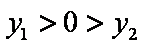
易知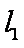
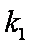
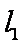
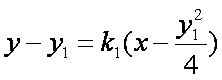
由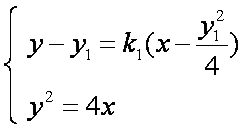

由直线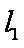

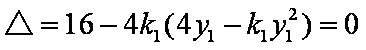
于是,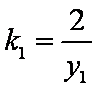
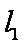
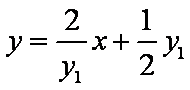
同理,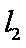
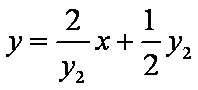
联立
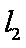
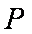
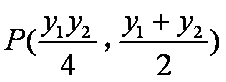
∵ 
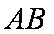

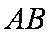

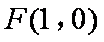
∴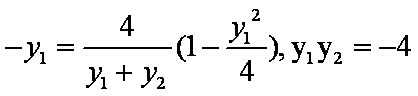
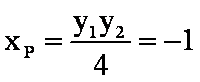
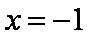
(2)由(1)知,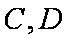
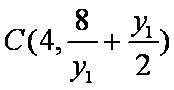
∴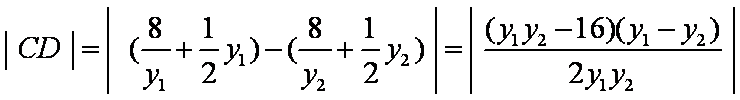
∴ 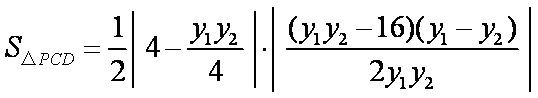
设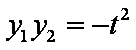
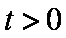
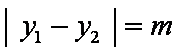
由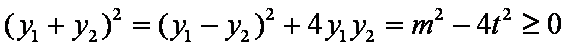
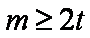
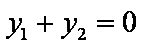
∴ 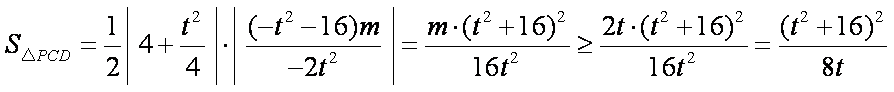
设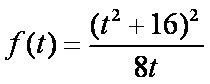
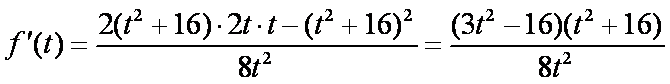
∴ 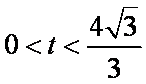
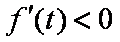
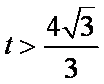
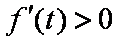
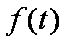
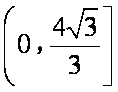
在区间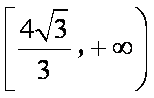
∴ 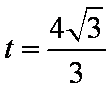
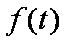
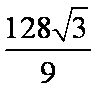
∴ 当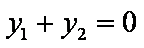
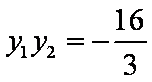
即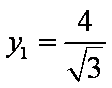

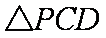
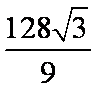
知识点
已知数列



(1)记

(2)数列
正确答案
(1)6;(2)491
解析
令


反之,由符合上述条件的八项数列

记符合条件的数列










(1)对于三种情况,易知当


(2)
知识点
设A,B为两个互不相同的集合,命题P:




正确答案
解析
由已知得,



知识点
函数


正确答案
解析
过点






,又





知识点
已知函数f(x)=log2

正确答案
解析
解:∵已知函数f(x)=log2


故函数f(x) 是奇函数,则f(﹣a)=﹣f(a)=﹣
故选 D。
知识点
在△ABC中,角A,B,C的对边分别为a,b,c,且
(1)求角B的大小;
(2)已知

正确答案
见解析
解析
解:(1)

∵

∴


(2)

∴


而
∴

知识点
设双曲线

正确答案
解析
依题由




又

知识点
扫码查看完整答案与解析