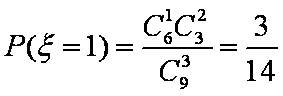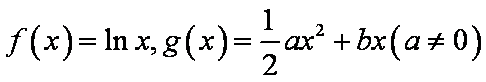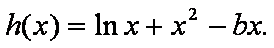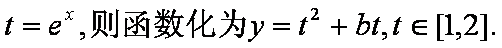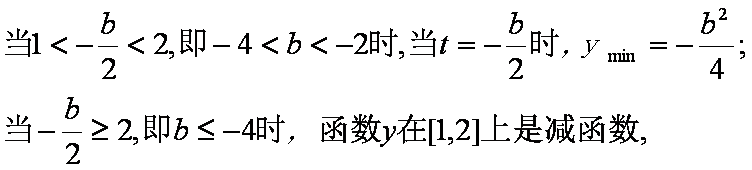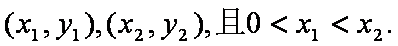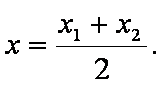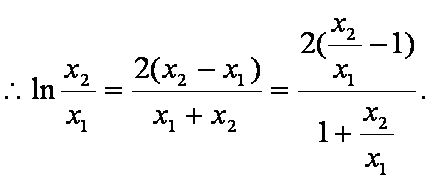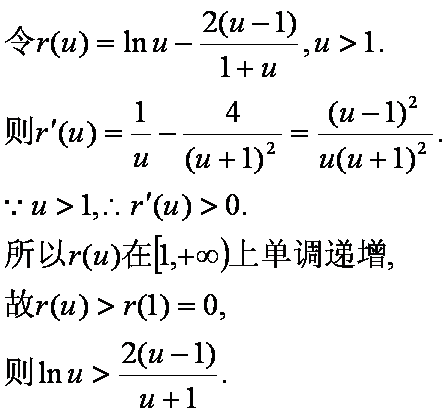导数的加法与减法法则
共661题

导数的加法与减法法则
共661题

热门试卷

题型：单选题

单选题 · 5 分

如图，B地在A地的正东方向4 km处，C地在B地的北偏东30°方向2 km处，河流的没岸PQ（曲线）上任意一点到A的距离比到B的距离远2 km.现要在曲线PQ上选一处M建一座码头，向B、C两地转运货物.经测算，从M到B、M到C修建公路的费用分别是a万元/km、2a万元/km，那么修建这两条公路的总费用最低是（）

A(2－2)a万元

B5a万元

C(2+1) a万元

D(2+3) a万元

正确答案

解析

依题意知PMQ曲线是以A、B为焦点、实轴长为2的双曲线的一支（以B为焦点），此双曲线的离心率为2，以直线AB为轴、AB的中点为原点建立平面直角坐标系，则该双曲线的方程为，点C的坐标为（3，）.则修建这条公路的总费用ω=a[|MB|+2|MC|]=2a[|MB|+|MC|],设点、在右准线上射影分别为点M 、C ，根据双曲线的定义有，所以。当且仅当点M在线段上时取等号，故ω的最小值是5a.

知识点

导数的加法与减法法则

题型：简答题

简答题 · 14 分

在△ABC中，角A、B、C所对的边分别为a,b，c，已知c=2。acosB－bcosA=。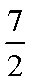

（1）求bcosA的值；

（2）若a=4，求△ABC的面积。

正确答案

见解析

解析

（1）∵，根据余弦定理得，，

∴ ，又∵ ，∴ ，

∴ .

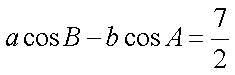
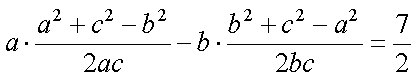
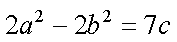
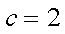
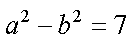
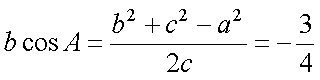
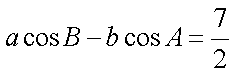
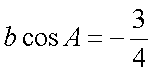
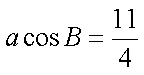
（2）由及，得.

又∵ ，∴ ，∴ ，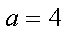

∴ .

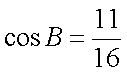
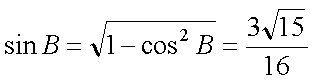
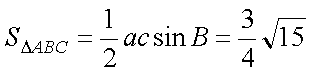
知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

已知集合，，则等于（）

正确答案

解析

由B得，因此选A

知识点

导数的加法与减法法则

题型：简答题

简答题 · 12 分

已知函数的定义域为R，其导数满足，常数为方程的实数根。

（1）求证：当时，总有成立；

（2）对任意，若满足求证：

正确答案

见解析。

解析

（1）令则

函数为R增函数

当时

当时，总有成立

（2）证明：

又

在是增函数

由（1）知：；

知识点

导数的加法与减法法则

题型：简答题

简答题 · 12 分

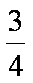
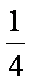
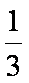
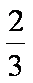
长沙市某中学在每年的11月份都会举行“社团文化节”，开幕式当天组织举行大型的文艺表演，同时邀请36名不同社团的社长进行才艺展示。其中有的社长是高中学生，的社长是初中学生，高中社长中有是高一学生，初中社长中有是初二学生。

（1）若校园电视台记者随机采访3位社长，求恰有1人是高一学生且至少有1人是初中学生的概率；

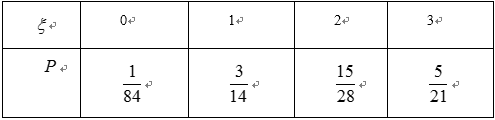
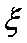
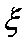
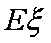
（2）若校园电视台记者随机采访3位初中学生社长，设初二学生人数为，求的分布列及数学期望。

正确答案

见解析。

解析

（1）由题意得，高中学生社长有27人，其中高一学生9人；初中学生社长有9人，其中初二学生社长6人。

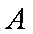
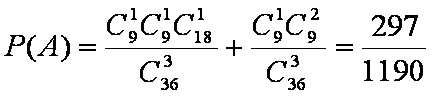
事件为“采访3人中，恰有1人是高一学生且至少有1人是初中学生”。

………6分

（2）的可能取值为0，1，2，3

，，

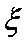
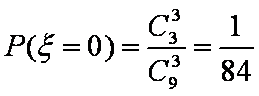
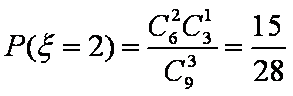
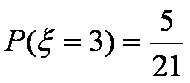
所以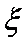的分布列为

所以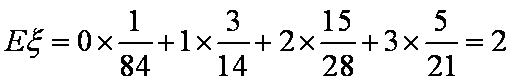………12分

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

某流程图如图所示，现输入如下四个函数，则可以输出的函数是

正确答案

解析

根据程序框图知输出的函数为奇函数，并且此函数存在零点，经验证：不存在零点；不存在零点；为偶函数，且的定义域为全体实数，且，故此函数为奇函数，且令，得，函数存在零点，答案C

知识点

导数的加法与减法法则

题型：简答题

简答题 · 13 分

已知焦点在x轴上的椭圆C1：的离心率互为倒数，它们在第一象限交点的坐标为，设直线（其中k,m为整数）。

（1）试求椭圆C1和双曲线C2 的标准方程；

（2）若直线l与椭圆C1交于不同两点A、B，与双曲线C2交于不同两点C、D，问是否存在直线l，使得向量，若存在，指出这样的直线有多少条？若不存在，请说明理由。

正确答案

见解析。

解析

（1）将点代入解得：

∴椭圆为：，

椭圆C的离心率为∴双曲线的离心率为，

∴ ，

∴双曲线为：

（2）由消去化简整理得：

设，，则

①

由消去化简整理得：

设，，则

②

因为，所以

由得：。

所以或，由上式解得或。

当时，由①和②得，因是整数，

所以的值为，，，，，，。

当，由①和②得，因是整数，所以，，。

于是满足条件的直线共有9条。

知识点

导数的加法与减法法则

题型：简答题

简答题 · 13 分

已知函数

（1）若时，函数在其定义域上是增函数，求的取值范围；

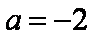
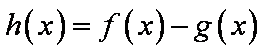
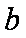
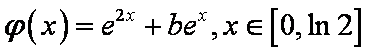
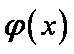
（2）在（1）的结论下，设函数，求函数的最小值；

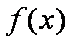
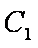
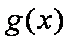
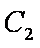
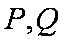
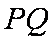
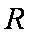
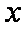
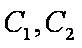
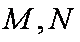
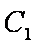
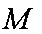
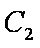
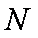
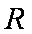
（3）设函数的图象与函数的图象交于点，过线段的中点作轴的垂线分别交于点，问是否存在点，使在处的切线与在处的切线平行？若存在，求出的横坐标；若不存在，请说明理由。

正确答案

见解析。

解析

（1）依题意：

在（0,+）上是增函数，

对x∈（0,+）恒成立， …………2分

…………4分

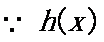
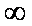
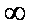
（2）设

当t=1时，ym I n=b+1；…………6分

当t=2时，ym I n=4+2b…………8分

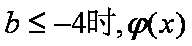
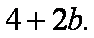
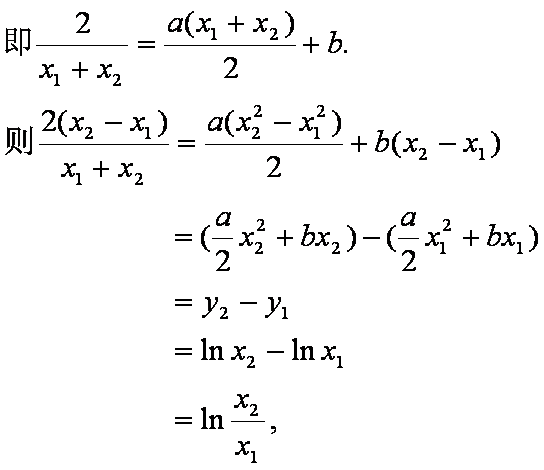
当的最小值为…………8分

（3）设点P、Q的坐标是

则点M、N的横坐标为

C1在点M处的切线斜率为

C2在点N处的切线斜率为…………9分

假设C1在点M处的切线与C2在点N处的切线平行，则

设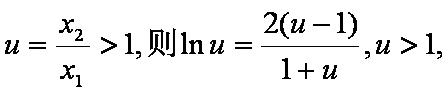 ①…………11分

这与①矛盾，假设不成立。

故C1在点M处的切线与C2在点N处的切线不平行…………13分

知识点

导数的加法与减法法则

题型：简答题

简答题 · 12 分

在△ABC中，角A，B，C所对的边分别为，已知函数 R）。

（1）求函数的最小正周期和最大值；

（2）若函数在处取得最大值，求的值。

正确答案

（1）函数的最小正周期是,最大值是

（2）

解析

（1）依题意，

所以函数的最小正周期是,有最大值。

（2）由（I）知：由，得，所以。

知识点

导数的加法与减法法则

题型：简答题

简答题 · 13 分

已知抛物线，过点的直线与抛物线交于、两点，且直线与交于点.

（1）求证: ，、成等比数列；

（2）设，，试问是否为定值，若是，求出此定值；若不是，请说明理由。

正确答案

见解析。

解析

（1）设直线的方程为：，

联立方程可得得: ①

设，，，则， ②

，

而，∴，

即，、成等比数列

（2）由，得，

，

即得：，，则

由（1）中②代入得，

故为定值且定值为

知识点

导数的加法与减法法则

继续学习学习下一知识点

下一知识点 : 导数的乘法与除法法则

百度题库 > 高考 > 理科数学 > 导数的加法与减法法则

扫码查看完整答案与解析