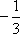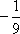- 导数的加法与减法法则
- 共661题
设函数
(1)对每个


(2)对任意


正确答案
见解析。
解析
(1) 

综上,对每个


(2) 由题知


知识点
等比数列{an}的前n项和为Sn.已知S3=a2+10a1,a5=9,则a1=( )。
正确答案
解析
设数列{an}的公比为q,若q=1,则由a5=9,得a1=9,此时S3=27,而a2+10a1=99,不满足题意,因此q≠1.
∵q≠1时,S3=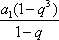
∴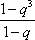
∵a5=a1·q4=9,即81a1=9,∴a1=
知识点
一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n。如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验。
假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为,且各件产品是否为优质品相互独立
(1)求这批产品通过检验的概率;
(2)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望。
正确答案
见解析
解析
设第一次取出的4件产品中恰有3件优质品为事件A,第一次取出的4件产品中全为优质品为事件B,第二次取出的4件产品都是优质品为事件C,第二次取出的1件产品是优质品为事件D,这批产品通过检验为事件E,根据题意有E=(AB)∪(CD),且AB与CD互斥,
∴P(E)=P(AB)+P(CD)=P(A)P(B|A)+P(C)P(D|C)=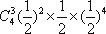
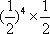
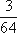
(2)X的可能取值为400,500,800,并且
P(X=400)=1-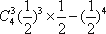


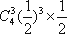

∴X的分布列为
EX=400×


知识点
设z=(2-i)2(i为虚数单位),则复数z的模为__________。
正确答案
5
解析
|z|=|(2-i)2|=|4-4i+i2|=|3-4i|=
知识点
设













正确答案
解析






知识点
扫码查看完整答案与解析