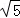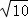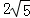- 由递推关系式求数列的通项公式
- 共176题
1
题型:填空题
|
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
1
题型:简答题
|
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(1)证明:PA⊥BD;
(2)若PD=AD,求二面角A-PB-C的余弦值。
正确答案
见解析
解析
(1)因为
从而BD2+AD2= AB2,故BD 


所以BD 

(2)如图,以D为坐标原点,AD的长为单位长,射线DA为

则



设平面PAB的法向量为n=(x,y,z),则

因此可取n=
设平面PBC的法向量为m,则
可取m=(0,-1,
故二面角A-PB-C的余弦值为
知识点
由递推关系式求数列的通项公式
1
题型:
单选题
|
设x,y∈R,向量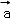
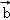
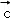

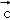
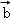


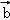
正确答案
B
解析
∵ 向量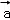
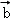
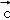
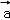
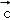
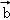
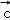
解得 x=2,y=﹣2,故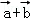
故有|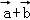
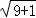
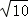
知识点
由递推关系式求数列的通项公式
1
题型:
单选题
|
设a∈z,且0≤a≤13,若512012+a能被13整除,则a=( )
正确答案
D
解析
∵512012+a=(52﹣1)2012+a
=


由于
要使得能512012+a能被13整除,且a∈Z,0≤a≤13
则可得a+1=13
∴a=12
故选D
知识点
由递推关系式求数列的通项公式
1
题型:填空题
|
执行右图所示的程序框图,输入l=2,m=3,n=5,则输出的y的值是 .
正确答案
68
解析
由输入l=2,m=3,n=5,计算得出y=278,第一次得新的y=173;第二次得新的y=68<105,输出y.
知识点
由递推关系式求数列的通项公式
下一知识点 : 由其它方法求数列的通项公式
扫码查看完整答案与解析