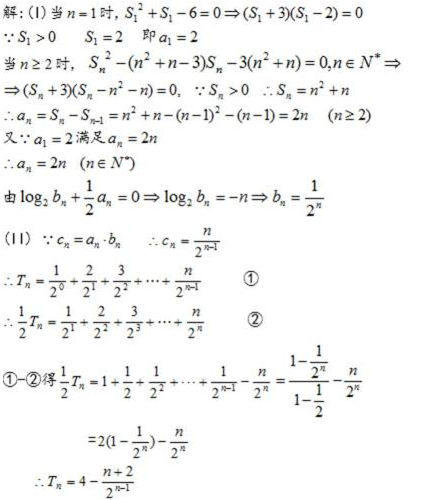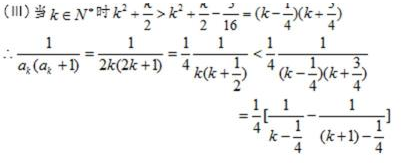- 由递推关系式求数列的通项公式
- 共176题
8.已知数列






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.对于函数








(1)判断函数
(2)已知







(3)在(2)的条件下,试比较

正确答案
(1)
∴
∴ 是“幅度函数”,其“幅度”为2
(2)
∵ 


∴ 当
当
∴ 
∴
(3)
令

∴
∴ 
解析
解析已在路上飞奔,马上就到!
知识点
21.设各项为正数的数列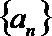

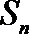

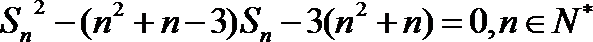
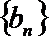
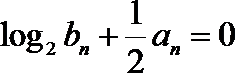
(Ⅰ)求数列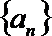
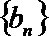
(Ⅱ)设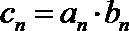
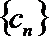

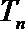
(Ⅲ) 证明:对一切正整数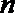
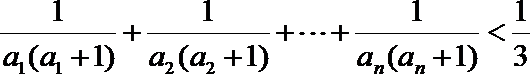
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在数列
(1)求数列

(2)若存在


正确答案
解:(1)
(2)
由(1)可知当
设
则
又

所以所求实数
解析
解析已在路上飞奔,马上就到!
知识点
26.设二次方程



(1)试用

(2)求证:
(3)当

正确答案
(1)根据韦达定理得



(2)因为
所以数列是等比数列
(3)当
所以
解析
解析已在路上飞奔,马上就到!
知识点
3.定义;称






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知等差数列{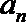
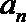
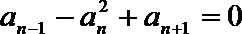
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设
(1)求实数a;
(2)求数列{xn}的通项公式;
(3)若
正确答案
(1)由
解析
解析已在路上飞奔,马上就到!
知识点
18.已知等差数列{an}中,首项a1=1,公差d为整数,且满足a1+3<a3,a2+5>a4,数列{bn}满足
(1)求数列{an}的通项公式an;
(2)若S2为S1,Sm(m∈N*)的等比中项,求正整数m的值.
正确答案
(1)由题意,得


又d∈Z,∴d = 2.∴an=1+(n-1)
(2)∵
∴
∵



∴

解得m=12.
解析
解析已在路上飞奔,马上就到!
知识点
21. 









(1)求函数
(2)设

(3)若(2)中数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析