由递推关系式求数列的通项公式
共176题

· 由递推关系式求数列的通项公式

由递推关系式求数列的通项公式
共176题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 18 分

23．已知数列的首项（是常数，且），（），数列的首项，（）．

（1）证明：从第2项起是以2为公比的等比数列；

（2）设为数列的前项和，且是等比数列，求实数的值；

（3）当时，求数列的最小项．

正确答案

（1）∵

∴

（n≥2）

由得，，

∵，∴ ，

即从第2项起是以2为公比的等比数列．

（2）

当n≥2时，

∵是等比数列，

∴（n≥2）是常数，

∴，即．

（3）由（1）知当时，，

所以，

，

显然最小项是前三项中的一项．

当时，最小项为；当时，最小项为或；

当时，最小项为．

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式等比数列的判断与证明等比数列的性质及应用数列与不等式的综合

题型：简答题

简答题 · 10 分

17．在数列中N其中．

（I）求数列的通项公式；

（II）求数列的前项和；

（III）证明存在N使得对任意N均成立．

正确答案

（I）解法一：，

，

．

由此可猜想出数列的通项公式为．

以下用数学归纳法证明．

（1）当时等式成立．

（2）假设当时等式成立，即

那么，

这就是说，当时等式也成立．

根据（1）和（2）可知，

等式对任何N都成立．

解法二：由N

可得

所以为等数列，其公差为1，首项为0．

故

所以数列的通项公式为

（II）

设 ①

②

当时，①式减去②式，得

这时数列的前项和

当时，这时数列的前项和

（III）通过分析，推测数列的第一项最大．

下面证明： ③

由知要使③式成立，只要因为

所以③式成立．

因此，存在使得对任意N均成立．

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式分组转化法求和数列与不等式的综合

题型：单选题

单选题 · 5 分

16．对于数列，如果存在正实数，使得数列中每一项的绝对值均不大于，那么称该数列为有界的，否则称它为无界的．在以下各数列中，无界的数列为（）

A，．

B，．

C，．

D，．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式数列与不等式的综合

题型：简答题

简答题 · 18 分

20．函数的定义域，对定义域内任意两个实数，都有成立．

（1）求的值并证明为偶函数；

（2）若，记，求数列的前2009项的和；

（3）若，且不等式对任意正实数恒成立，求非零实数a的取值范围．

正确答案

（1）赋值得，

为偶函数

（2）得，

；

，

（3）设，

，

得

恒成立，

又，

从而

解析

解析已在路上飞奔，马上就到！

知识点

函数奇偶性的判断抽象函数及其应用函数的值由递推关系式求数列的通项公式数列与不等式的综合

题型：简答题

简答题 · 12 分

16．设等差数列{an}的前n项和为Sn，且S4＝4S2，a2n＝2an＋1．

（Ⅰ）求数列{an}的通项公式；

（Ⅱ）证明：对一切正整数n，有．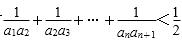

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式等差数列的基本运算等差数列的性质及应用裂项相消法求和数列与不等式的综合

题型：简答题

简答题 · 16 分

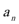
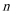
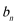
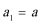
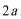
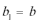
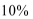
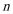
21．政府决定用“对社会的有效贡献率”对企业进行评价用表示某企业第年投入的治理污染的环保费用，用表示该企业第年的产值设（万元），以后治理污染的环保费用每年都比上一年增加（万元）；又设（万元,且企业的产值每年比上一年的平均增长率为，用表示企业第年“对社会的有效贡献率”。

（1）求该企业第一年和第二年的“对社会的有效贡献率”；

（2）试问：从第几年起该企业“对社会的有效贡献率”不低于？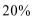

正确答案

（1）因为，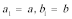

根据题意：，,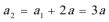

所以 ,,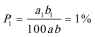

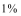
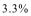
该企业第一年和第二年的“对社会的有效贡献率”分别为和;

（2）因为 , ,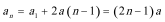

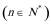
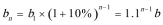
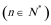
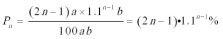
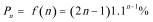
所以 ,下证：为增函数:

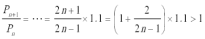
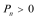
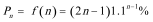
证法1：, , 则为增函数;

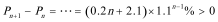
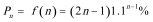
证法2：,∴,则为增函数,

再验证：， ,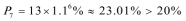

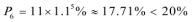
故，从第七年起该企业“对社会的有效贡献率”不低于

解析

解析已在路上飞奔，马上就到！

知识点

函数模型的选择与应用由递推关系式求数列的通项公式数列与函数的综合

题型：单选题

单选题 · 5 分

7．数列1，，，……，的前n项和为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式裂项相消法求和

题型：单选题

单选题 · 5 分

12．已知数列的通项公式是，其中a、b均为正常数，那么与的大小关系是（）

D与n的取值相关

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式数列与不等式的综合

题型：简答题

简答题 · 12 分

17．在数列中，

（I）证明是等比数列，并求的通项公式；

（II）求的前n项和。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式等比数列的判断与证明错位相减法求和

题型：简答题

简答题 · 14 分

22．已知数列{an}的前n项和，且=1，.

（I）求数列{an}的通项公式；

（II）已知定理：“若函数f（x）在区间D上是凹函数，x>y（x,y∈D），且f’（x）存在，则有< f’（x）”．若且函数y=xn+1在（0,+∞）上是凹函数，试判断bn与bn+1的大小；

（III）求证：≤bn<2.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由an与Sn的关系求通项an由递推关系式求数列的通项公式数列与函数的综合数列与不等式的综合

继续学习学习下一知识点

下一知识点 : 由其它方法求数列的通项公式

百度题库 > 高考 > 理科数学 > 由递推关系式求数列的通项公式

扫码查看完整答案与解析