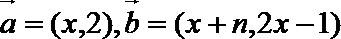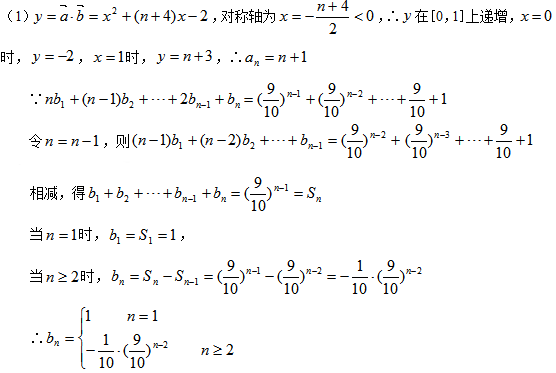- 由递推关系式求数列的通项公式
- 共176题
1
题型:填空题
|
8.在数列{an}中,a1=6,且对任意大于1的正整数n,点(



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
由递推关系式求数列的通项公式裂项相消法求和
1
题型:简答题
|
19.已知数列{



(Ⅰ)令


(Ⅱ)求数列

(Ⅲ)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
由递推关系式求数列的通项公式等差数列的判断与证明等比数列的判断与证明数列与解析几何的综合
1
题型:简答题
|
19.设向量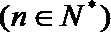
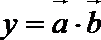
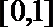
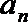
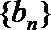
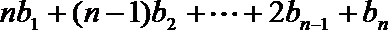
(1)求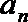
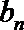
(2)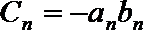
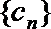
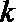
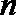
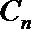
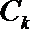
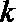
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
二次函数在闭区间上的最值平面向量数量积的运算由递推关系式求数列的通项公式数列与函数的综合数列与不等式的综合
1
题型:填空题
|
13.已知数列


正确答案
4,5,32
解析
解析已在路上飞奔,马上就到!
知识点
由递推关系式求数列的通项公式
1
题型:简答题
|
23.有三种卡片分别写有数字1,10和100。设m为正整数,从上述三种卡片中选取若干张,使得这些卡片上的数字之和为m。考虑不同的选法种数,例如当m=11时,有如下两种选法:“一张卡片写有1,另一张卡片写有10”或“11张写有1的卡片”,则选法种数为2。
(1)若m=100,直接写出选法种数;
(2)设n为正整数,记所选卡片的数字和为100n的选法种数为an 当n≥2时,求数列{an}的通项公式。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
由递推关系式求数列的通项公式数列与函数的综合计数原理的应用
下一知识点 : 由其它方法求数列的通项公式
扫码查看完整答案与解析