- 由递推关系式求数列的通项公式
- 共176题
5.设0<θ<
A2sin
B2sin
C2cos
D2cos
正确答案
解析
由已知得x1=2sin(
则x2=
x3=
…,xn=2cos
知识点
8.已知数列{bn}中,bn+1=
正确答案
4与0
解析
由b1=0,得
所以
当n为奇数时, 
则当n=1时,b1=0最小,
同时,最大值不存在,无限的趋近于1.
当n为偶数时, 
则当n=2时,b2=2最大,
此时,最小值不存在,无限的趋近于1.
综上可知,数列{bn}的最大项为b2=4,最小项为b1=0.
知识点
3.在数列{an}中,an+1=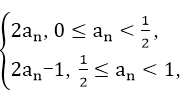
A
B
C
D
正确答案
解析
∵a1=
知识点
10.已知数列 (n∈N*)满足
正确答案
解析
由于t<a1<t+1,
得a2=a1-t,
易得0<a1-t<1,
即0<a2<1,又t>2,
那么a3=t+2-a2=2t+2-a1,
又t+1<2t+2-a1<t+2,
即
又1<t+2-a1<2,
即1<a4<2,
得a4<t,
从而a5=t+2-a4=a1,
结合
可得实数k的最小值为4.
知识点
14.已知数列 的前n项和Sn=10n-n2(n∈N+),则数列 的前n项和Tn为 .
正确答案
解析
当n=1时,a1=S1=9;当n≥2时,an=Sn-Sn-1=11-2n,
由于n=1时,a1=9也满足11-2n,
因此an=11-2n.
(1)当n>5时,
(2)当n≤5时,
综合(1)(2),得
知识点
扫码查看完整答案与解析