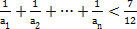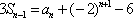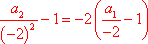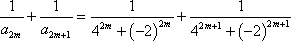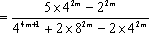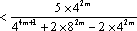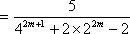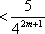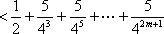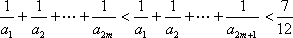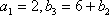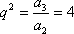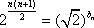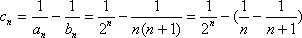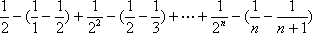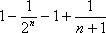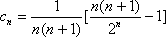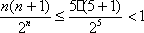- 由递推关系式求数列的通项公式
- 共176题
设数列

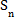
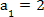
(1)求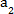
(2)求数列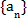
(3)证明:对一切正整数n,有
正确答案
见解析。
解析
解(1) 依题意, 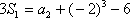
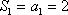

(2) 当
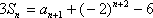
两式相减得
整理得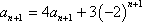

又因为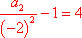
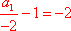
故数列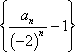
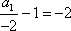
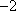
所以
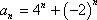
(3)因为当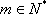
①当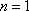
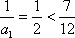
②当

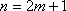
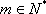
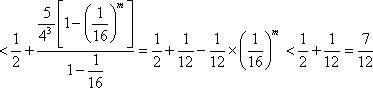
③当
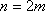
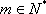
此时
综上,对一切正整数
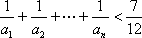
知识点
已知数列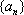
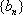
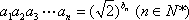
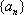
(1) 求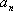
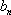
(2) 设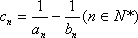


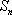
(i)求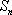
(ii)求正整数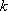
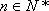
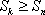
正确答案
见解析
解析
(1)∵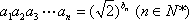
当n≥2,n∈N*时,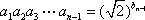
由①②知:当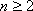
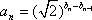
∵b3=6+b2, ∴a3=8。
∵{an}为等比数列,且a1=2,∴{an}的公比为q,则
由题意知an>0,∴q>0,∴q=2。
∴an=2n(n∈N*)。
又由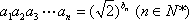
即
∴bn=n(n+1)(n∈N*)。
(2)(i)∵
∴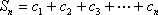
=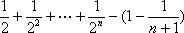
=
(ii)因为c1=0,c2>0,c3>0,c4>0;
当n≥5时,
而
所以,当n≥5时,cn<0,
综上,对任意n∈N*恒有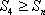
知识点
如果函数





正确答案
解析
求


知识点
已知数列



(1)求

(2)求
(3)设




正确答案
见解析。
解析
(1)当


当


(2)(法一)当


①—②得:





另解:
又



(法二)根据


用数学归纳法证明如下:
(1)当

(2)假设当

那么当

即:
又 
①-②得:
解,得


因此,由数学归纳法证得
(3)


知识点
已知数列


(1)求
(2)求

(3)记数列




正确答案
(1)3,13,39(2)
解析
(1)


(2)由题知,有

∴
(3) ∵
∴
∴
又






综上,有
知识点
设












正确答案
解析
略
知识点
已知数列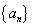

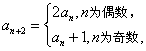

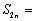
正确答案
7;
解析
略
知识点
设














正确答案
解析
因为



知识点
已知向量序列:




若


正确答案
9;3
解析
略
知识点
设数列





(1)当

(2)当

正确答案
(1)3个;(2)393个
解析
(1)当


所以



所以满足条件的所有数列
(2)令


反之符合上述条件的7项数列
记符合条件的数列
显然




当



故
所以满足条件的所有数列
知识点
扫码查看完整答案与解析