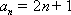- 由递推关系式求数列的通项公式
- 共176题
若数列


正确答案
解析
略
知识点
已知公差不为0的等差数列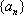

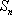
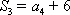
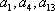

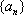
(2)求数列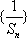

正确答案
(1)
(2)
解析
(1)设等差数列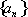
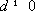
因为
所以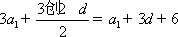
因为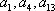
所以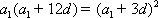
由①,②可得: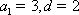
所以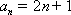
(2)由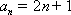
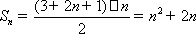
……………………………………9分
所以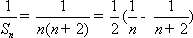
所以
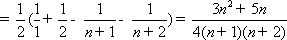
所以数列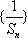

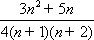
知识点
若


正确答案
解析
略
知识点
数列

正确答案
解析
略
知识点
已知数列
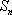
(1)求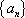
(2)设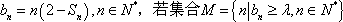
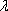
正确答案
见解析
解析
知识点
已知数列







(1)判断数列

(2)求
正确答案
见解析。
解析
(1)




所以




(2)由(1)可知







知识点
正项数列




正确答案
解析
略
知识点
已知数列


正确答案
解析
略
知识点
设


正确答案
解析
略
知识点
已知等差数列



(1)求数列

(2)记



(注:


正确答案
见解析。
解析
(1)因为等差数列
所以
即
所以
(2)由(1)知

因为




所以
当

当

综上可知,
知识点
扫码查看完整答案与解析