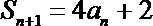- 由递推关系式求数列的通项公式
- 共176题
19.已知数列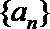



(1)求数列
(2)设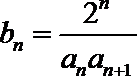




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知数列{an}为等差数列,且满足an+1=an2-nan+1,n=1,2,3,…
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求证:
(Ⅲ)当





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(1) 求
(2) 若



正确答案
(1)


(2)
解析
解析已在路上飞奔,马上就到!
知识点
16.数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设有

(1)求数列{xn}的通项公式;
(2)若
(3)是否存在最小整数m,使得对任意n∈N*,有
正确答案
(1)因方程f(x)=x有唯一解,可求a=

数列{


故

所以数列{xn}的通项公式为
(2)将xn代入an可求得an=2n-1,所以
(3)
即要
解析
解析已在路上飞奔,马上就到!
知识点
19.已知


(Ⅰ)判断函数
(Ⅱ) 求证:
(Ⅲ) 已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.数列




(1)求数列
(2)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
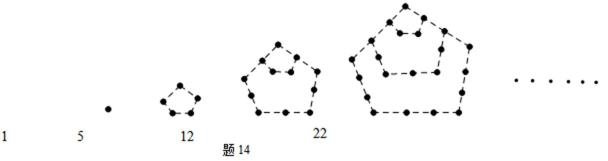
14. 两千多年前,古希腊毕达哥拉

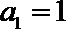







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知函数










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.设数列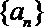
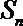
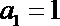
(1)设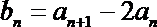
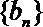
(2)求数列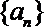
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析