- 由递推关系式求数列的通项公式
- 共176题
1
题型:简答题
|
20.已知
(I)求证:数列{an,-1)是等比数列;
(Ⅱ)当n取何值时,bn取最大值,并求出最大值;
(Ⅲ)若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
由递推关系式求数列的通项公式等差数列的判断与证明数列与不等式的综合
1
题型:简答题
|
19.各项都为正数的数列{an},满足a1=1,
(1)求数列{an}的通项公式;
(2)求数列
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
由递推关系式求数列的通项公式错位相减法求和
1
题型:简答题
|
18. 已知数列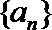
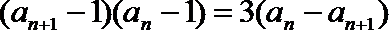

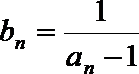
(Ⅰ)证明:数列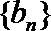
(Ⅱ)求数列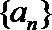
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
由递推关系式求数列的通项公式等差数列的判断与证明
1
题型:
单选题
|
11.数列{an}的首项为3,{bn}为等差数列且bn=an+1-an(n∈N*).若b3=-2,b10=12,则a8=( )
正确答案
B
解析
知识点
由递推关系式求数列的通项公式等差数列的性质及应用
1
题型:简答题
|
20.已知数列{an}中,a1=t(t∈R,且t≠0,1),a2=t2,且当x=t时,函数f(x)=
(Ⅰ)求证:数列{an+1-an}是等比数列;
(Ⅱ)若bn=anln|an|(n∈N),求数列{bn}的前n项和Sn;
(Ⅲ)当t=-
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
由递推关系式求数列的通项公式等比数列的判断与证明数列与不等式的综合
下一知识点 : 由其它方法求数列的通项公式
扫码查看完整答案与解析