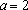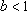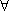- 抛物线的定义及应用
- 共187题
已知圆锥母线长为6,底面圆半径长为4,点





(1)当


(2)当三棱锥

正确答案
(1)

解析
(1) 连





又









当


当


综上异面直线



(2)







又


知识点
已知圆


正确答案
解析
略
知识点
已知曲线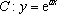
(1)若曲线C在点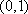
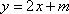

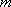
(2)对任意实数

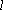
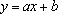
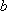
正确答案
(1) 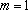
(2) b的取值范围是
解析
(1)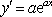
因为曲线C在点(0,1)处的切线为L: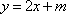
所以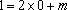
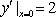
解得

(2)法1:
对于任意实数a,曲线C总在直线的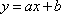
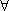
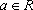
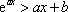
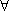
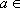
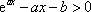
令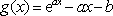
①若a=0,则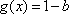
所以实数b的取值范围是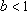
②若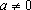
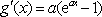
由
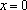
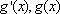
------------------------------------11分
所以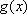

所以实数b的取值范围是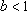
综上,实数b的取值范围是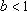
法2:对于任意实数a,曲线C总在直线的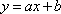
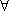
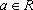
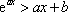
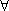
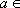
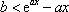
令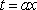
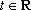

令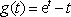
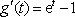
由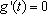
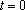

------------------------------------11分
所以 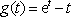
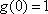
实数b的取值范围是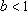
知识点
已知抛物线的方程为




(1)求抛物线的方程;
(2)已知


(3)设点B、C是抛物线上的动点,点D是抛物线与
正确答案
见解析。
解析
(1)
设点A(3,-1)关于直线

则
把点

所以抛物线的方程为
(2)∵
∴抛物线的准线为
过点M作准线的垂线,垂足为A,由抛物线的定义知
∴

即当点M为过点P所作的抛物线准线的垂线与抛物线的交点时,
∴

(3)BC所在的直线经过定点,该定点坐标为
令
设

则
∵

直线BC的方程为
即
所以直线BC经过定点
知识点
如图,直线










(1)用





(2)求




(3)小张所在的兴趣小组完成上面两个小题后,小张连








正确答案
见解析
解析
(1)由

点
设切线方程为




由于



(2)






(本小题也可以求


(3)由(1)知









记





所以封闭图形的面积
知识点
扫码查看完整答案与解析