- 抛物线的定义及应用
- 共187题
设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点PA⊥l,A为垂足,如果AF的斜率为-
正确答案
8
解析
抛物线的焦点为F(2,0),准线为x=-2,因为PA⊥准线l,设P(m,n),则
A(-2,n),因为AF的斜率为-





知识点
设斜率为1的直线l过抛物线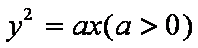
正确答案
16
解析
依题意,有F(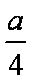
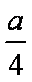
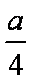
△OAF的面积为: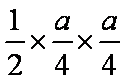
知识点
已知点A是抛物线y2=2px(p>0)上一点,F为抛物线的焦点,准线l与x轴交于点K,已知|AK|=
(1)求p的值;
(2)过该抛物线的焦点作两条互相垂直的直线l1,l2,与抛物线相交得两条弦,两条弦
的中点分别为G,H.求|GH|的最小值。
正确答案
(1)4(2)8
解析
解析:(1)设
因为抛物线的焦点
则


又
(2)由



设



由 


=

所以
知识点
已知直线



(1)求实数
(2)问点


正确答案
见解析。
解析
(1)将


由△

另一方面,弦长AB

(2)当

则只须使得
即

知识点
已知抛物线


正确答案
解析
依题意,得F(p,0),因为AF







知识点
扫码查看完整答案与解析









