- 抛物线的定义及应用
- 共187题
1
题型:填空题
|
已知双曲线





正确答案
解析
略
知识点
抛物线的定义及应用
1
题型:
单选题
|
设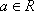
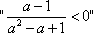
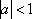
正确答案
C
解析
略
知识点
抛物线的定义及应用
1
题型:填空题
|
若直线









正确答案
解析
略
知识点
抛物线的定义及应用
1
题型:
单选题
|
若抛物线


正确答案
B
解析

知识点
抛物线的定义及应用
1
题型:简答题
|
在平面直角坐标系xOy中,F是抛物线C:x2=2py(p>0)的焦点,M是抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为
(1)求抛物线C的方程;
(2)是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M的坐标;若不存在,说明理由;
(3)若点M的横坐标为



正确答案
见解析。
解析
(1)F抛物线C:x2=2py(p>0)的焦点F






(2)假设存在点M,使得直线MQ与抛物线C相切于点M,
而




由



即


(3)若点M的横坐标为


由


圆

于是

设

当

即当

故当

知识点
抛物线的定义及应用
下一知识点 : 抛物线的标准方程和几何性质
扫码查看完整答案与解析










