- 抛物线的定义及应用
- 共187题
已知P,Q为抛物线

正确答案
-4
解析
因为点P,Q的横坐标分别为4,
由




知识点
设




(1)求抛物线
(2)

















正确答案
(1)y2=4x(2)4
解析
(1)设

则



所以


(2)设


则


所以
设AC所在直线方程为
联立


同理

所以
设AB所在直线方程为


所以 
知识点
过抛物线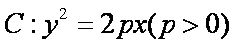
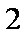


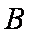
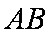
直径的圆与
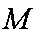
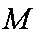
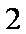
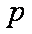
正确答案
解析
略
知识点
已知抛物线














(1)求证:

(2)若











正确答案
见解析
解析
解析:(1)设


所以



所以







(2)设

由
同理
所以面积
设

由


得到

②得

所以当


所以当




所以

知识点
已知动圆的圆心C在抛物线x2=2py(p>0)上,该圆经过点A(0,p),且与x轴交于两点M、N,则sin∠MCN的最大值为 。
正确答案
1
解析
解析 : 由题意,设C(x0,y0),则⊙C的方程(x﹣x0)2+(y﹣y0)2=x02+(y0﹣p)2。
把y=0和x02=2py0代入整理得x2﹣2x0x+x02+p2=0。
设M、N的横坐标分别为x1、x2,则x1=x0﹣p,x2=x0+p,∴|MN|=|x1﹣x2|=2p。
∵|CM|=|CN|=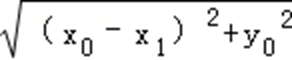
∴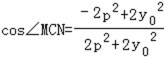

∵ 0<∠MCN<π∴ 0<sin∠MCN≤1,
∴ sin∠MCN的最大值为1故答案为:1
知识点
扫码查看完整答案与解析












