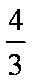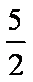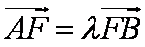- 抛物线的定义及应用
- 共187题
过抛物线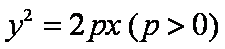
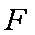
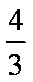
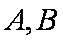
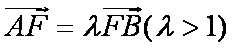
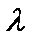
正确答案
解析
据题意设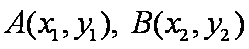
由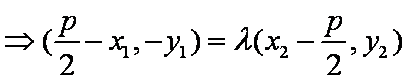
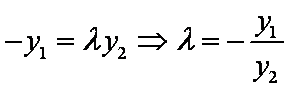
联立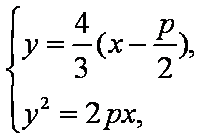
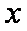
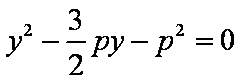
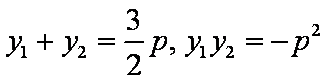
∴
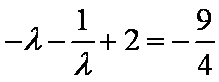
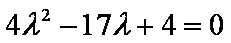
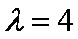
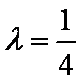
知识点
如图,已知抛物线



(1)求抛物线
(2)过点







正确答案
见解析
解析
(1)

所以

故


(2)设


则

所以

同理,




即
由


所以直线

于是
令


所以,

知识点
抛物线
正确答案
解析

知识点
如图,设椭圆




(1)若抛物线上存在点

(2)若





正确答案
见解析
解析
(1)
由四边形
得
且


所以椭圆方程为
(2)
不妨设

因为
所以


又因为直线



所以

联立方程组


所以点

所以
又


知识点
已知抛物线

(1)求抛物线C的方程;
(2)以M点为起点的任意两条射线l1,l2的斜率乘积为l,并且l1与抛物线C交于A、B两点,l2与抛物线C交于D、E两点,线段AB、DE的中点分别为G、H两点,求证:直线GH过定点,并求出定点坐标。
正确答案
见解析
解析
解:(1)∵

又∵点N在抛物线C上,∴62=18p,解得p=2。
∴抛物线C的方程为y2=4x。
2)由题意可知:直线l1,l2的斜率存在且不为0,
设l1:y=k(x﹣12)+8,则l2:
由
是A(x1,y1),B(x2,y2),则
又y1+y2=k(x1+x2﹣24)+16,
∴x1+x2=
∴线段AB的中点G
用
∴kGH=


∴直线GH:
令y=0,得到x=10。
∴直线GH过定点(10,0)。
知识点
扫码查看完整答案与解析