- 导数的几何意义
- 共149题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知函数f(x)=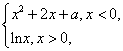
(1)指出函数f(x)的单调区间;
(2)若函数f(x)的图象在点A,B处的切线互相垂直,且x2<0,求x2-x1的最小值;
(3)若函数f(x)的图象在点A,B处的切线重合,求a的取值范围。
正确答案
见解析
解析
(1)函数f(x)的单调递减区间为(-∞,-1),单调递增区间为[-1,0),(0,+∞)。
(2)由导数的几何意义可知,点A处的切线斜率为f′(x1),点B处的切线斜率为f′(x2),
故当点A处的切线与点B处的切线垂直时,有f′(x1)f′(x2)=-1.
当x<0时,对函数f(x)求导,得f′(x)=2x+2.
因为x1<x2<0,
所以,(2x1+2)(2x2+2)=-1.
所以2x1+2<0,2x2+2>0.
因此x2-x1=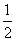
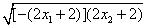
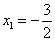

所以,函数f(x)的图象在点A,B处的切线互相垂直时,x2-x1的最小值为1.
(3)当x1<x2<0或x2>x1>0时,f′(x1)≠f′(x2),故x1<0<x2.
当x1<0时,函数f(x)的图象在点(x1,f(x1))处的切线方程为y-(x12+2x1+a)=(2x1+2)(x-x1),即y=(2x1+2)x-x12+a.
当x2>0时,函数f(x)的图象在点(x2,f(x2))处的切线方程为y-ln x2=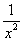
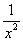
两切线重合的充要条件是
由①及x1<0<x2知,-1<x1<0.
由①②得,a=x12+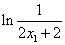
设h(x1)=x12-ln(2x1+2)-1(-1<x1<0),
则h′(x1)=2x1-
所以,h(x1)(-1<x1<0)是减函数。
则h(x1)>h(0)=-ln 2-1,
所以a>-ln 2-1.
又当x1∈(-1,0)且趋近于-1时,h(x1)无限增大,
所以a的取值范围是(-ln 2-1,+∞)。
故当函数f(x)的图象在点A,B处的切线重合时,a的取值范围是(-ln 2-1,+∞)。
知识点
设曲线y=ax-ln(x+1)在点(0,0)处的切线方程为y=2x,则a=( )
正确答案
解析
知识点
设



(1)求曲线

(2)设

正确答案
(1)
(2)
解析
(1)因

令


又令


因此
又因为



(2)由(1)知,

令

当



当



当



从而函数



知识点
设函数
(1)当a=1时,求
(2)若


正确答案
见解析。
解析
对函数求导得:
(1)单调性的处理,通过导数的零点进行穿线判别符号完成。
当a=1时,令
当

(2)区间
待定量a的值。
当

最大值在右端点取到。
知识点
扫码查看完整答案与解析










