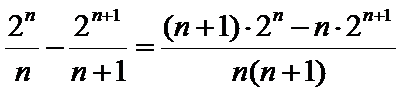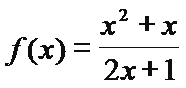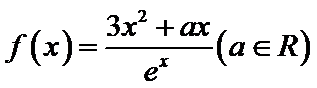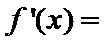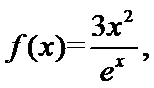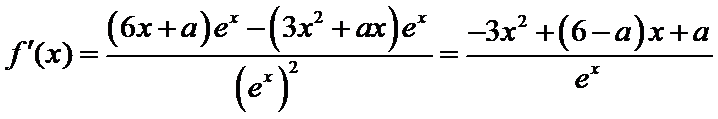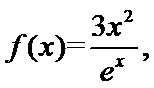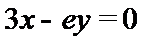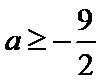- 导数的几何意义
- 共149题
10.已知
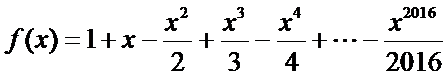
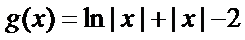
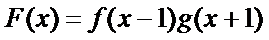
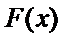
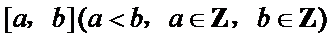
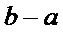
正确答案
解析
由题意,得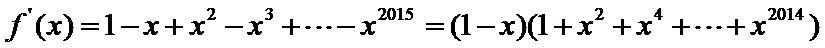
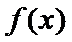
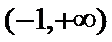
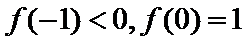
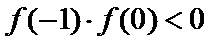
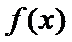
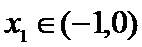
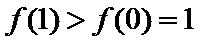
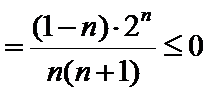
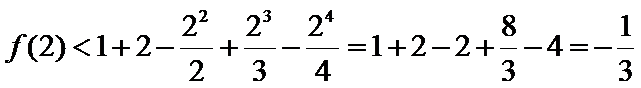
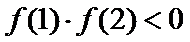
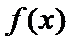
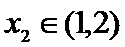
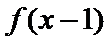
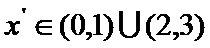


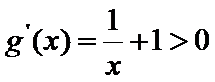
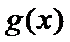
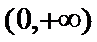
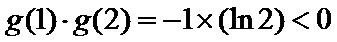
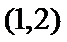
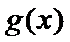
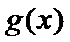
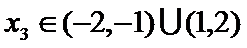
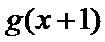
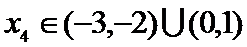
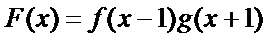
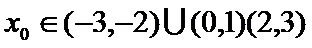

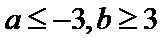
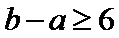
考查方向
解题思路
1)求导,判断两函数的单调性;
2)利用零点存在定理得到两函数的零点所在区间;
3)求函数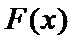
易错点
本题易在判断两函数的单调性时出现错误,易忽视“利用导数的符号确定函数的单调性”.
知识点
8.设函数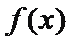
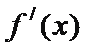

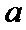



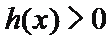

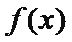
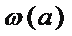
①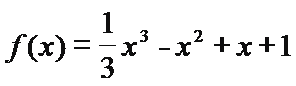
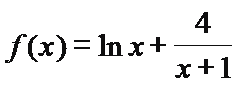
③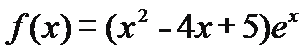
其中具有性质
正确答案
解析
①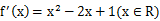
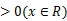
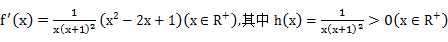
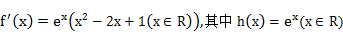
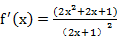
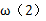
考查方向
解题思路
分别对函数求导,变形与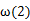
易错点
不理解函数新信息的性质而出错
知识点
19.已知函数

(1)证明:当|a|≥2时,M(a,b)≥2;
(2)当a
正确答案
(1)详见解析;(2)3;
解析
试题分析:(1)分析题意可知





(1)由f(x)= 














(2)由M(a,b)








考查方向
解题思路
(1)根据a的取值范围,得到函数在[-1,1]上的单调性,分类讨论证得结论;(2)由题中给出的新定义进行求解.
易错点
二次函数在闭区间上的单调性.
知识点
(本小题满分12分,(1)小问7分,(2)小问5分)
设函数
23.若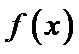
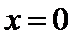
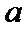
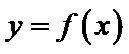
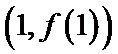
24.若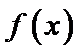
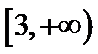
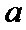
正确答案
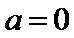
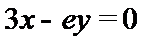
解析
试题分析:本题考查求复合函数的导数,导数与函数的关系,由求导法则可得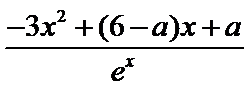
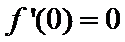
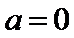
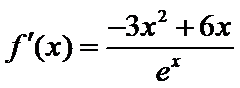
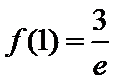
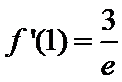
试题解析:(1)对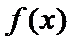
因为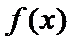
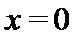
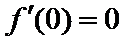
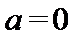
当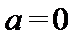
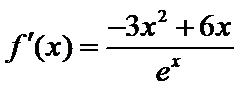
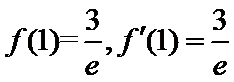
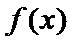
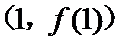
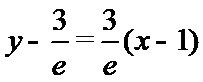
考查方向
解题思路
导数及其应用通常围绕四个点进行命题.第一个点是围绕导数的几何意义展开,设计求曲线的切线方程,根据切线方程求参数值等问题,这类试题在考查导数的几何意义的同时也考查导数的运算、函数等知识,试题的难度不大;第二个点是围绕利用导数研究函数的单调性、极值(最值)展开,设计求函数的单调区间、极值、最值,已知单调区间求参数或者参数范围等问题,在考查导数研究函数性质的同时考查分类与整合思想、化归与转化思想等数学思想方法.
易错点
极值的几何意义.
正确答案
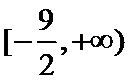
解析
试题分析:(2)由题意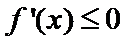
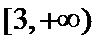
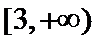
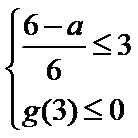
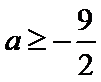
试题解析:(2)由(1)得,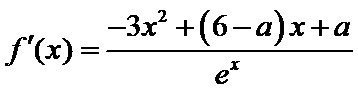
令
由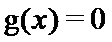
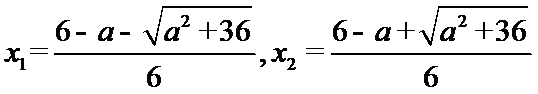
当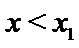
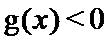
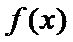
当
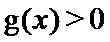
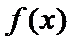
当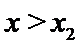
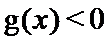
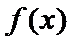
由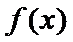
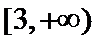
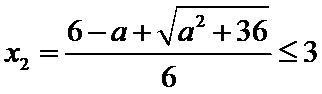
故a的取值范围为
考查方向
解题思路
导数及其应用通常围绕四个点进行命题.第三个点是围绕导数研究不等式、方程展开,涉及不等式的证明、不等式的恒成立、讨论方程根等问题,主要考查通过转化使用导数研究函数性质并把函数性质用来分析不等式和方程等问题的能力,该点和第二个点一般是解答题中的两个设问,考查的核心是导数研究函数性质的方法和函数性质的应用;第四个点是围数性质并把函数性质用来分析不等式和方程等问题的能力,该点和第二个点一般是解答题中的两个设问,考查的核心是导数研究函数性质的方法和函数性质的应用;
易错点
本题涉及第一个点和第二个点,主要注意问题的转化,转化为不等式恒成立,转化为二次函数的性质.
已知函数
27.设
28.证明:存在




正确答案
当






解析
由已知,函数


所以
当


在区

当


解题思路
首先对函数




易错点
不会确定分类的标准导致出错或不分类;
正确答案
详见解析.
解析
由

令
则
故存在

令
由


所以
即
当

由(1)知,函数

故当


当


所以,当

综上所述,存在




考查方向
解题思路
要使得













因为










当



故当







易错点
找不到解决问题的思路导致无法入手。
扫码查看完整答案与解析