- 导数的几何意义
- 共149题
已知函数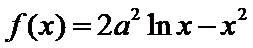

当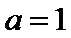
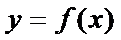
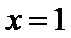
讨论函数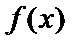
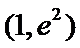

正确答案
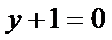
解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)求导,然后算出在切点处的导数值,求出切线方程;当 
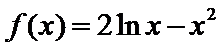
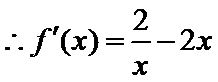
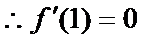
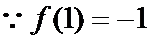
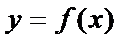
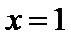
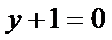
考查方向
解题思路
本题考查导数的应用,解题步骤如下:求导,然后算出在切点处的导数值,求出切线方程。
易错点
忽略函数的定义域导致出错。
正确答案
当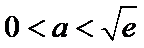
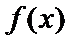
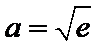
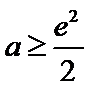
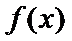
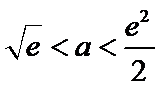
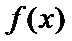
解析
试题分析本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,要注意对参数的讨论。∵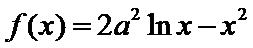
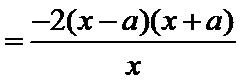
因为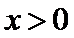
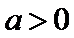

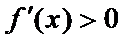
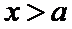
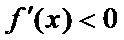
所以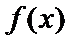
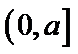
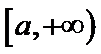
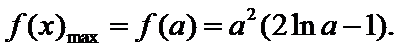
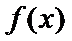
①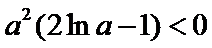
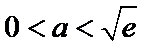

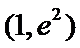
②当
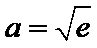
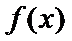
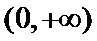
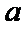
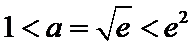
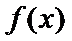
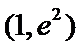
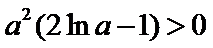
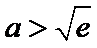

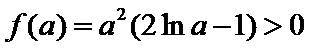
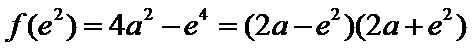

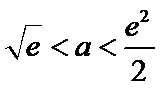

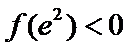
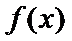
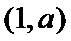
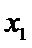
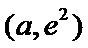
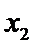
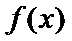
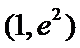
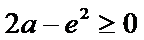
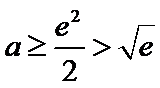
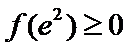
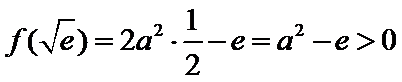

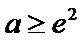
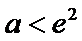
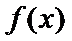
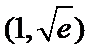
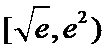
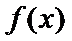
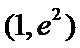
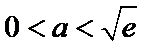
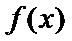
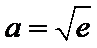

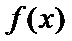
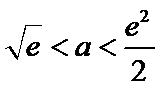
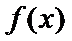
考查方向
解题思路
本题考查导数的应用,解题步骤如下:算出定义域,对参数分类讨论分析单调性,确定最值,再由图确定零点的个数。
易错点
第二问中的易丢对a的分类讨论。
已知函数
26.若函数


27.若斜率为






正确答案

解析



因为函数




解得
考查方向
解题思路
直接求导,


易错点
函数的恒成立问题,构造新函数;用导数解决函数的综合性问题
正确答案
证明略
解析
设点



要证
即证










即

考查方向
解题思路
设出交点坐标,用分析法证明,要证



易错点
函数的恒成立问题,构造新函数;用导数解决函数的综合性问题
已知函数
26.当

27.当




正确答案
当



当


当



解析


①当










②当




③当





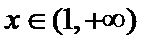

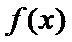
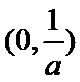
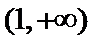
综上,当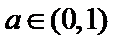
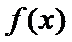

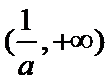
当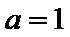
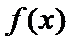
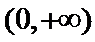
当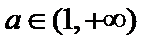
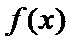
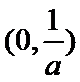
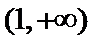
考查方向
解题思路
解题步骤如下:先求函数的导数,根据导函数的正负来讨论原函数的单调性,但是要讨论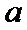
易错点
本题易在分类讨论和解含参数的不等式时发生错误 。
正确答案

解析


即关于


令函数

令函数

上有








当






考查方向
解题思路
解题步骤如下:要证



易错点
本题不容易构造函数,讨论其单调性,求其范围,导致题目无法进行。
已知函数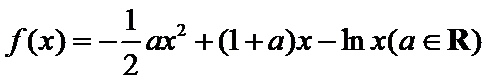
26.当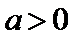
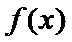
27.当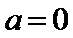
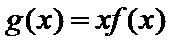
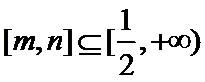
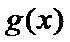
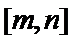

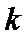

正确答案
当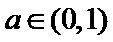
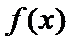
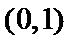
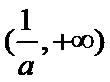
当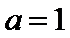

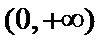
当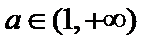
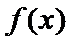

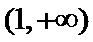
解析
【解析】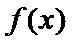
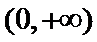
①当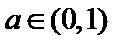
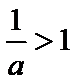
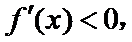
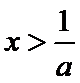
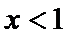
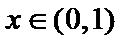
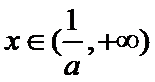
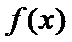
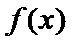
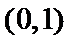
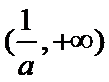
② 当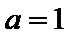
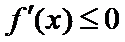
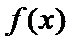
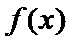
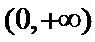
③ 当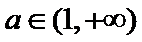
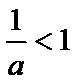
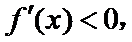
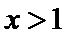
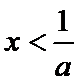
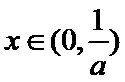
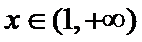
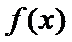
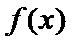
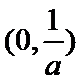
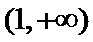
综上,当
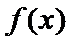
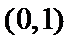
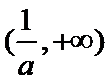
当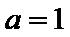
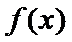
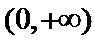
当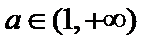
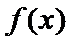
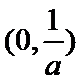
考查方向
解题思路
解题步骤如下:先求函数的导数,根据导函数的正负来讨论原函数的单调性,注意讨论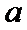
易错点
本题易在分类讨论和解含参数的不等式时发生错误 。
正确答案
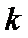
解析
当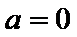
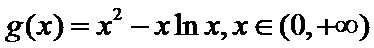
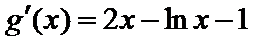
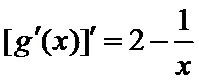
当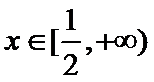
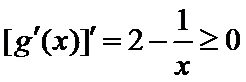
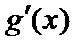
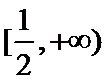
又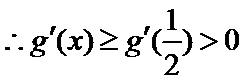

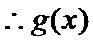
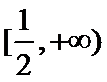
由题意,得
原问题转化为关于
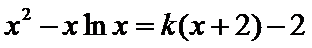
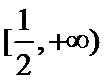
即方程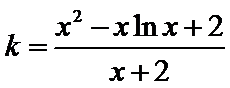
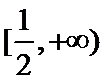
令函数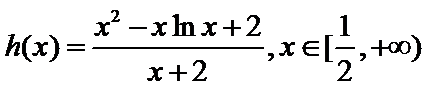
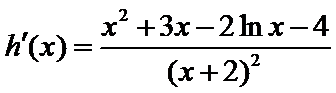
令函数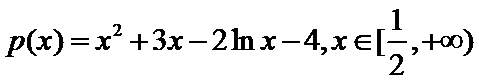
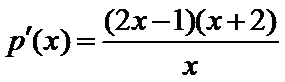
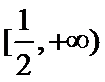
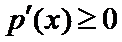
故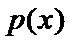
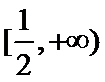
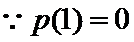
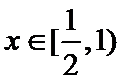
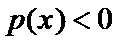
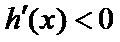
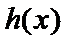
当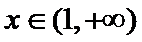

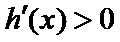
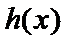
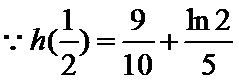
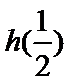
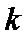
考查方向
解题思路
解题步骤如下:根据函数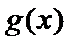
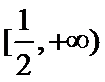
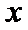

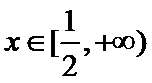
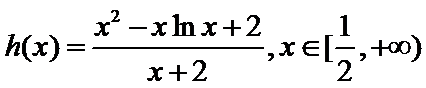
易错点
本题不容易构造函数,讨论其单调性,求其范围,导致题目无法进行。
12.已知函数


正确答案
解析
(1).当m=0,n=0时,f(x)=

(2).当m=0,n







考查方向
解题思路
根据函数的特点,从特殊值入手,(1).当m=0,n=0;当m=0,n
易错点
不理解{x| f(x)=0}={x| f(f(x))=0 }
知识点
扫码查看完整答案与解析