- 导数的几何意义
- 共149题
已知函数f(x)=x3+ax2+b(a,b∈R).
25.试讨论f(x)的单调性;
26.若b=c﹣a(实数c是与a无关的常数),当函数f(x)有三个不同的零点时,a的取值范围恰好是(﹣∞,﹣3)∪(1,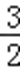
正确答案
函数f(x)在(﹣∞,0),(﹣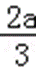
解析
(1)∵f(x)=x3+ax2+b,
∴f′(x)=3x2+2ax,
令f′(x)=0,可得x=0或﹣
a=0时,f′(x)>0,∴f(x)在(﹣∞,+∞)上单调递增;
a>0时,x∈(﹣∞,﹣

∴函数f(x)在(﹣∞,﹣
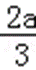
a<0时,x∈(﹣∞,0)∪(﹣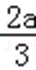
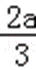
∴函数f(x)在(﹣∞,0),(﹣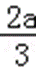
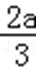
考查方向
解题思路
(1)求导数,分类讨论,利用导数的正负,即可得出f(x)的单调性;
易错点
本题考查导数知识的综合运用,考查函数的单调性,分类讨论中易错
正确答案
c=1
解析
(2)由(1)知,函数f(x)的两个极值为f(0)=b,f(﹣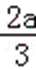
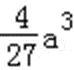
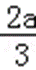
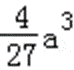
∵b=c﹣a,
∴a>0时,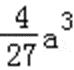
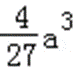
设g(a)=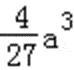
∵函数f(x)有三个不同的零点时,a的取值范围恰好是(﹣∞,﹣3)∪(1,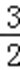
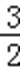
∴在(﹣∞,﹣3)上,g(a)<0且在(1,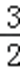
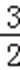
∴g(﹣3)=c﹣1≤0,且g(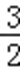
∴c=1,
此时f(x)=x3+ax2+1﹣a=(x+1)[x2+(a﹣1)x+1﹣a],
∵函数有三个零点,
∴x2+(a﹣1)x+1﹣a=0有两个异于﹣1的不等实根,
∴△=(a﹣1)2﹣4(1﹣a)>0,且(﹣1)2﹣(a﹣1)+1﹣a≠0,
解得a∈(﹣∞,﹣3)∪(1,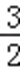
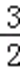
综上c=1.
考查方向
解题思路
(2)由(1)知,函数f(x)的两个极值为f(0)=b,f(﹣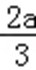
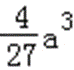
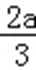
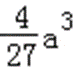
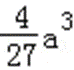
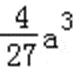
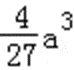
易错点
本题考查导数知识的综合运用,考查函数的单调性,考查函数的零点,在用范围的过程中易错.
已知函数f(x)=x3+ax2+b(a,b∈R).
25.试讨论f(x)的单调性;
26.若b=c﹣a(实数c是与a无关的常数),当函数f(x)有三个不同的零点时,a的取值范围恰好是(﹣∞,﹣3)∪(1,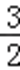
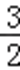
正确答案
函数f(x)在(﹣∞,0),(﹣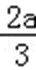
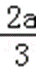
解析
(1)∵f(x)=x3+ax2+b,
∴f′(x)=3x2+2ax,
令f′(x)=0,可得x=0或﹣
a=0时,f′(x)>0,∴f(x)在(﹣∞,+∞)上单调递增;
a>0时,x∈(﹣∞,﹣

∴函数f(x)在(﹣∞,﹣
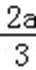
a<0时,x∈(﹣∞,0)∪(﹣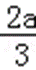
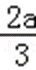
∴函数f(x)在(﹣∞,0),(﹣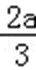
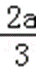
考查方向
解题思路
(1)求导数,分类讨论,利用导数的正负,即可得出f(x)的单调性;
易错点
本题考查导数知识的综合运用,考查函数的单调性,分类讨论中易错
正确答案
c=1
解析
(2)由(1)知,函数f(x)的两个极值为f(0)=b,f(﹣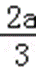
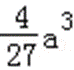
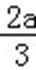
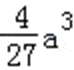
∵b=c﹣a,
∴a>0时,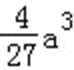
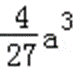
设g(a)=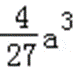
∵函数f(x)有三个不同的零点时,a的取值范围恰好是(﹣∞,﹣3)∪(1,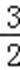
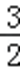
∴在(﹣∞,﹣3)上,g(a)<0且在(1,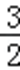
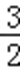
∴g(﹣3)=c﹣1≤0,且g(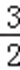
∴c=1,
此时f(x)=x3+ax2+1﹣a=(x+1)[x2+(a﹣1)x+1﹣a],
∵函数有三个零点,
∴x2+(a﹣1)x+1﹣a=0有两个异于﹣1的不等实根,
∴△=(a﹣1)2﹣4(1﹣a)>0,且(﹣1)2﹣(a﹣1)+1﹣a≠0,
解得a∈(﹣∞,﹣3)∪(1,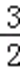
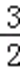
综上c=1.
考查方向
解题思路
(2)由(1)知,函数f(x)的两个极值为f(0)=b,f(﹣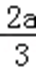
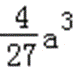
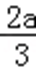
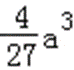
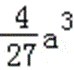
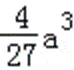
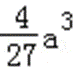
易错点
本题考查导数知识的综合运用,考查函数的单调性,考查函数的零点,在用范围的过程中易错.
12.设定义在




正确答案
解析
f(x)的定义域为
因为
所以
所以
所以
所以f(x)在区域内单调递增,所以既无极大值也无极小值
考查方向
利用导数求函数的极值
解题思路
先求定义域,然后求导,然后判断函数单调性
然后求出函数的极值
易错点
求导错误,判断极值时错误
教师点评
有极大值不一定有最大值,有最大值也不一定有极大值
知识点
已知函数
25.当

26.当


正确答案
令



故
解析
参见答案,注意适当的放缩不等式。
考查方向
不等式、函数、导数结合题,利用导数判断函数的单调性,进而证明不等式
解题思路
先构造正确的函数,然后对函数求导,求导后求出函数的单调区间,利用函数的单调性证明不等式。
易错点
不能够造出正确的函数,求导错误,算单调区间错误。
教师点评
本题的关键在于构造出正确的函数,然后求导利用函数单调性方可证明不等式
正确答案
当


当

所以

令
令
当

令




因此


所以,当

当

令




因此,


所以,当

综上,当



解析
详见答案,构造不等式函数时要适当
考查方向
函数导数不等式的综合题,不等式恒成立求参数的取值范围
解题思路
根据x的不同取值,将不等式化简变形,够造出新的函数,然后求导判断单调区间,利用单调性证明不等式,利用不等式恒成立,再讨论参数K的取值范围。
易错点
分类讨论有重复或有遗漏,计算错误。判断函数符号错误
教师点评
主要是构造出正确的不等式(函数)形式,本题的难点在于分类讨论时,要综合考虑所有的情况。
已知函数


25.求实数
26.用




正确答案
详见解析
解析
(1)对

设直线



解得

考查方向
导数的几何意义 利用导数求曲线的切线
解题思路
对
易错点
求导错误,想不到利用导数求曲线的切线
教师点评
导数是求曲线的切线的一个工具
正确答案
详见解析
解析
(2)记函数

对函数

当

当

从而
∴



∵

又曲线



∴
∴
从而
∴
由函数





①当




记

当


∴
故“



②当




综合(1)(2)知,当

故实数

考查方向
导数与函数的综合题,利用导数求函数的单调性
利用函数和导数证明不等式
解题思路
先利用导数判断函数的单调性及单调区间,利用函数的零点存在性定理及其单调性,分类讨论x的不同取值,进而判断实数C的取值范围
易错点
计算能力弱,求导错误,不能构造出恰当的函数
教师点评
这类题根据题意和已知条件,按逻辑分类讨论相关参数的值,最后综合所有出现的可能情况,得到答案
扫码查看完整答案与解析
















